求证:以 ,
,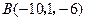 ,
,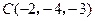 为顶点的三角形是等腰直角三角形.
为顶点的三角形是等腰直角三角形.
数列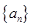 的前
的前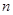 项和为
项和为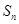 ,
, ,
,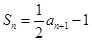
 .
.
(1)求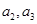 ;
;
(2)求数列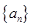 的通项
的通项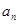 ;
;
(3)求数列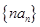 的前
的前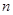 项和
项和 .
.
已知命题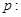 方程
方程 在
在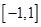 上有解;命题
上有解;命题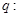 不等式
不等式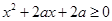 恒成立,若命题“
恒成立,若命题“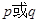 ”是假命题,求
”是假命题,求 的取值范围.
的取值范围.
设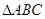 的内角
的内角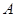 ,
, ,
,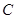 所对的边长分别为
所对的边长分别为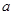 ,
,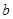 ,
,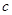 ,且
,且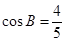 ,
, .
.
(1)当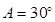 时,求
时,求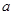 的值;
的值;
(2)当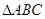 的面积为
的面积为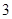 时,求
时,求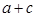 的值.
的值.
若函数 在
在 上为增函数(
上为增函数( 为常数),则称
为常数),则称 为区间
为区间 上的“一阶比增函数”,
上的“一阶比增函数”, 为
为 的一阶比增区间.
的一阶比增区间.
(1) 若 是
是 上的“一阶比增函数”,求实数
上的“一阶比增函数”,求实数 的取值范围;
的取值范围;
(2) 若 (
( ,
, 为常数),且
为常数),且 有唯一的零点,求
有唯一的零点,求 的“一阶比增区间”;
的“一阶比增区间”;
(3)若 是
是 上的“一阶比增函数”,求证:
上的“一阶比增函数”,求证: ,
,
如图,椭圆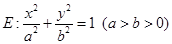 的左焦点为
的左焦点为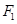 ,右焦点为
,右焦点为 ,过
,过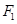 的直线交椭圆于
的直线交椭圆于 两点,
两点,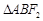 的周长为8,且
的周长为8,且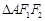 面积最大时,
面积最大时,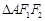 为正三角形.
为正三角形.
(1)求椭圆 的方程;
的方程;
(2)设动直线 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点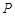 ,且与直线
,且与直线 相交于点
相交于点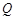 ,证明:点
,证明:点 在以
在以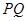 为直径的圆上.
为直径的圆上.