如下图,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(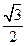 ,
, ,0),点D在平面yoz上,且
,0),点D在平面yoz上,且 BDC=900,
BDC=900, DCB=300,求点D的坐标。
DCB=300,求点D的坐标。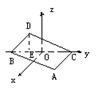
设函数
.
(I)求
的值域;
(II)记
的内角
的对边长分别为
,若
,求
的值.
已知以原点
为中心,
为右焦点的双曲线
的离心率
.
(Ⅰ)求双曲线
的标准方程及其渐近线方程;
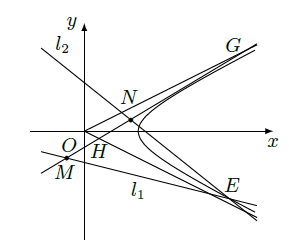
(Ⅱ)如题图,已知过点
的直线
与过点
(其中
)的直线
:
的交点
在双曲线
上,直线
与双曲线的两条渐近线分别交于
、
两点,求
的值.
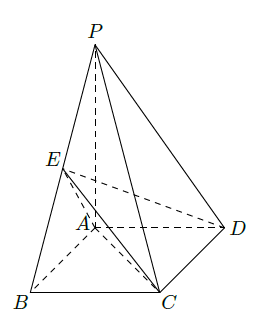
如图,四棱锥
中,底面
为矩形,
底面
,
,点
是棱
的中点.
(Ⅰ)证明:
平面
;
(Ⅱ)若
,求二面角
已知函数
(其中常数
),
是奇函数.
(Ⅰ)求
的表达式;
(Ⅱ)讨论
的单调性,并求
在区间[1,2]上的最大值和最小值.
设
的内角
的对边长分别为
,且
.
(Ⅰ) 求
的值;
(Ⅱ)求
的值.