在我军的一场模拟空战演习中,我军甲、乙、丙三名飞行员向同一假想敌机炮击,已知甲乙丙三名飞行员击中敌机的概率分别为0.4、0.5和0.7。
(1)求敌机被击中的概率;
(2)若一名飞行员击中,敌机坠毁的概率是0.2,若两名飞行员击中,敌机坠毁的概率是0.6,若三名飞行员击中,则敌机必然坠毁,求敌机坠毁的概率。
(本小题满分12分) 已知圆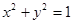 过椭圆
过椭圆 的两焦点,与椭圆有且仅有两个公共点;直线
的两焦点,与椭圆有且仅有两个公共点;直线 与圆
与圆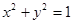 相切 ,与椭圆
相切 ,与椭圆 相交于
相交于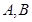 两点记
两点记
(1)求椭圆的方程;
(2)求 的取值范围;
的取值范围;
(3)求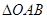 的面积S的取值范围.
的面积S的取值范围.
(本小题满分12分) 已知椭圆E: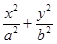 =1(a>b>o)的离心率e=
=1(a>b>o)的离心率e=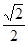 ,且经过点(
,且经过点( ,1),O为坐标原点。
,1),O为坐标原点。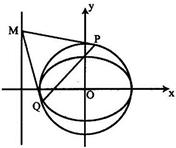
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)圆O是以椭圆E的长轴为直径的圆,M是直线x=-4在x轴上方的一点,过M作圆O的两条切线,切点分别为P、Q,当∠PMQ=60°时,求直线PQ的方程.
(本小题满分12分) 已知点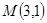 ,直线
,直线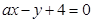 及圆
及圆 .
.
(1)求过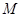 点的圆的切线方程;
点的圆的切线方程;
(2)若直线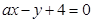 与圆相切,求
与圆相切,求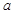 的值;
的值;
(3)若直线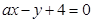 与圆相交于
与圆相交于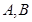 两点,且弦
两点,且弦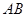 的长为
的长为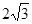 ,求
,求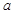 的值.
的值.
(本小题满分12分) 已知圆 过两点
过两点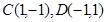 ,且圆心
,且圆心 在
在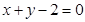 上.
上.
(1)求圆 的方程;
的方程;
(2)设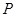 是直线
是直线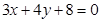 上的动点,
上的动点, 是圆
是圆 的两条切线,
的两条切线,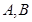 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值.
(本小题满分12分)已知两点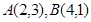 ,直线
,直线 ,在直线
,在直线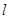 上求一点
上求一点 .
.
(1)使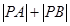 最小;(2)使
最小;(2)使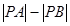 最大.
最大.