如图所示, 四棱锥P ABCD底面是直角梯形,
ABCD底面是直角梯形,  底面ABCD, E为PC的中点, PA=AD=AB=1.
底面ABCD, E为PC的中点, PA=AD=AB=1. 
(1)证明:  ;
;
(2)证明:  ;
;
(3)求三棱锥B PDC的体积V.
PDC的体积V.
四棱锥A-BCDE的正视图和俯视图如下,其中正视图是等边三角形,俯视图是直角梯形.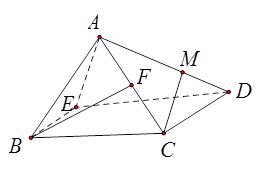
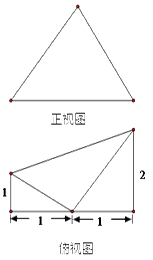
(Ⅰ)若F为AC的中点,当点M在棱AD上移动,是否总有BF丄CM,请说明理由.
(Ⅱ)求三棱锥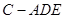 的高.
的高.
已知等比数列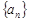 是递增数列,
是递增数列,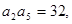
 ,数列
,数列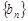 满足
满足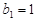 ,且
,且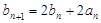 (
(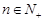 )
)
(Ⅰ)证明:数列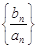 是等差数列;
是等差数列;
(Ⅱ)若对任意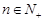 ,不等式
,不等式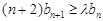 总成立,求实数
总成立,求实数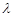 的最大值.
的最大值.
在△ABC中,角A,B,C所对的边分别为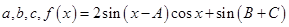
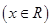 ,函数
,函数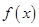 的图象关于点
的图象关于点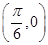 对称.
对称.
(Ⅰ)当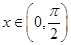 时,求
时,求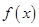 的值域;
的值域;
(Ⅱ)若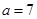 且
且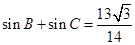 ,求△ABC的面积.
,求△ABC的面积.
已知数列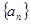 ,当
,当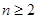 时满足
时满足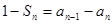 ,
,
(Ⅰ)求该数列的通项公式;
(Ⅱ)令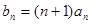 ,求数列
,求数列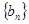 的前n项和
的前n项和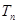 .
.
已知函数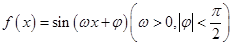 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数 的解析式,并写出
的解析式,并写出 的单调减区间;
的单调减区间;
(Ⅱ)已知 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且 的值.
的值.