已知抛物线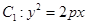 与椭圆
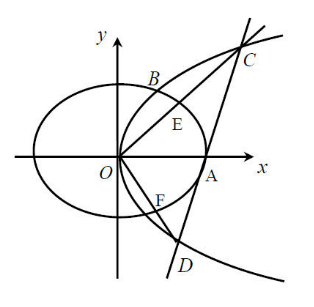
与椭圆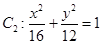 在第一象限的交点为B,O为坐标原点,A是椭圆右顶点,
在第一象限的交点为B,O为坐标原点,A是椭圆右顶点,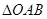 的面积为
的面积为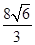 .
.
(1)求抛物线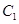 的方程;
的方程;
(2)过A点作直线 交
交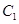 于C,D两点,射线OC,OD分别交
于C,D两点,射线OC,OD分别交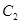 于E,F两点,记
于E,F两点,记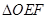 和
和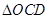 的面积分别为
的面积分别为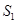 和
和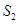 ,问是否存在直线
,问是否存在直线 ,使得
,使得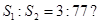 若存在,求出直线
若存在,求出直线 方程,若不存在,请说明理由.
方程,若不存在,请说明理由.
.(本小题满分l4分)已知函数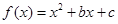 有唯一的零点
有唯一的零点 .
.
(1)求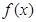 的表达式;
的表达式;
(2)若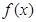 在区间
在区间 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围;
(3)若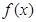 在区间
在区间 上的最大值为4,求
上的最大值为4,求 的值。
的值。
(本小题满分l4分)已知函数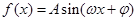 (其中
(其中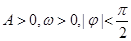 )的图象如下图所示。
)的图象如下图所示。
(1)求 ,
, 及
及 的值;
的值;
(2)若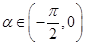 ,且
,且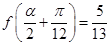 ,求
,求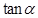 的值.。
的值.。
(本小题满分l2分)已知函数 。
。
(1)求函数 的最小正周期;
的最小正周期;
(2)若 ,且
,且 ,求
,求 的值。
的值。
(本小题12分)已知函数
(1)求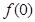 的值;
的值;
(2)求函数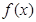 的最大值,并求
的最大值,并求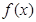 取最大值时
取最大值时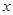 取值的集合;
取值的集合;
(3)求函数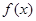 的单调增区间。
的单调增区间。
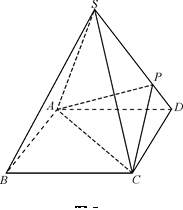
如图8所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的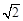 倍,点P在侧棱SD上,且
倍,点P在侧棱SD上,且 .
.
(Ⅰ)求证:AC⊥SD;
(Ⅱ)求二面角P-AC-D的大小;
(Ⅲ)侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.