已知函数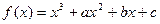 的图象过原点,且在x=1处取得极值,直线
的图象过原点,且在x=1处取得极值,直线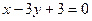 与曲线
与曲线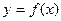 在原点处的切线互相垂直。
在原点处的切线互相垂直。
(I)求函数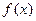 的解析式;
的解析式;
(II)若对任意实数的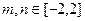 ,恒有
,恒有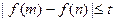 成立,求实数t的取值范围。
成立,求实数t的取值范围。
已知函数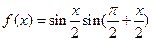
⑴求函数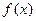 在[
在[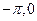 ]上的单调区间;
]上的单调区间;
⑵已知角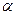 满足
满足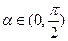 ,
,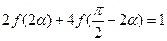 ,求
,求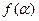 的值。
的值。
已知函数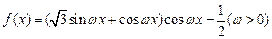 最小正周期为
最小正周期为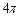
(1)求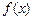 的单调递增区间
的单调递增区间
(2)在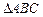 中,角
中,角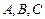 的对边分别是
的对边分别是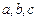 ,满足
,满足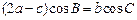 ,求函数
,求函数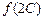 的取值范围
的取值范围
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA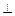 底面ABCD,点M是棱PC的中点,AM
底面ABCD,点M是棱PC的中点,AM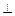 PBD.
PBD.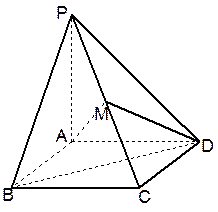
(1)求PA的长
(2)证明PB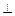 平面AMD
平面AMD
(3)求棱PC与平面AMD所成角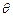 的余弦值.
的余弦值.
设函数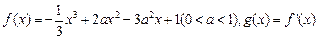 .
.
(1)求函数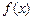 的极大值
的极大值
(2)若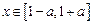 时,恒有
时,恒有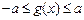 成立,试确定实数
成立,试确定实数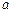 的取值范围.
的取值范围.
在平面直角坐标系中,已知点 ,向量
,向量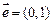 ,点B为直线
,点B为直线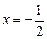 上的动点,点C满足
上的动点,点C满足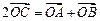 ,点M满足
,点M满足 .
.
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在 轴上,圆
轴上,圆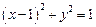 内切于
内切于 ,求
,求 的面积的最小值.
的面积的最小值.