分别求出经过点P(3,4)且满足下列条件的直线方程,并画出图形.
①斜率k=2;②与x轴平行;③与x轴垂直.
有四个数:前三个成等差数列,后三个成等比数列。首末两数和为16,中间两数和为12。求这四个数。
如图,三棱柱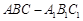 中,侧面
中,侧面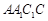
 底面
底面 ,
, ,且
,且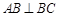 ,O为
,O为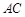 中点.
中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求直线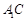 与平面
与平面 所成角的正弦值
所成角的正弦值
袋子中装有编号为a,b的2个黑球和编号为c,d,e的3个红球,从中任意摸出2个球.
(Ⅰ)写出所有不同的结果;
(Ⅱ)求恰好摸出1个黑球和1个红球的概率;
(Ⅲ) 求至少摸出1个黑球的概率.
已知数列{an}各项均为正数,Sn为其前n项和,对于 ,总有
,总有 成等差数列.
成等差数列.
(I )求数列{an}的通项an;
(II)设数列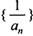 的前n项和为Tn,数列{Tn}的前n项和为Rn,求证:
的前n项和为Tn,数列{Tn}的前n项和为Rn,求证: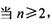
 时,
时, ;
;
(III)对任意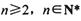 ,试比较
,试比较 与
与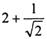 的大小
的大小
在ΔABC中,顶点A,B, C所对三边分别是a,b,c已知B(-1, 0), C(1, 0),且b,a, c成等差数列.
(I )求顶点A的轨迹方程;
(II) 设顶点A的轨迹与直线y=kx+m相交于不同的两点M、N,如果存在过点P(0,-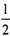 )的直线l,使得点M、N关于l对称,求实数m的取值范围
)的直线l,使得点M、N关于l对称,求实数m的取值范围