已知
，
的图象向右平移
个单位再向下平移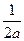
个单位后得到函数
的图象。
（Ⅰ）求函数的表达式；（Ⅱ）当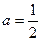
时，求在区间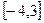
上的最大值与最小值；
（ Ⅲ）若函数
上的最小值为
的最大值。
已知函数f（x）＝ln
－a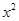
＋x（a＞0）．
（Ⅰ）若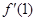
＝
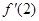，求f（x）图像在x＝1处的切线的方程；
（Ⅱ）若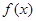
的极大值和极小值分别为m，n，证明：
．
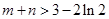已知椭圆长轴的左右端点分别为A，B，短轴的上端点为M，O为椭圆的中心，F为椭圆的右焦点，且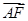
·
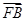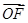＝1，｜
｜＝1．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若直线l交椭圆于P，Q两点，问：是否存在直线l，使得点F恰为△PQM的垂心?若存在，求出直线l的方程；若不存在，请说明理由．
如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，AE＝1，CD与平面ABDE所成角的正弦值为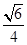
．
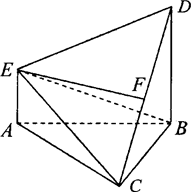
（Ⅰ）若F是线段CD的中点，证明：EF⊥面DBC;
（Ⅱ）求二面角D－EC－B的平面角的余弦值．
甲、乙两人参加某种选拔测试．在备选的10道题中，甲答对其中每道题的概率都是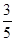
，乙能答对其中的5道题．规定每次考试都从备选的10道题中随机抽出3道题进行测试，答对一题加10分，答错一题（不答视为答错）减5分，得分最低为0分，至少得15分才能入选．
（Ⅰ）求乙得分的分布列和数学期望；
（Ⅱ）求甲、乙两人中至少有一人入选的概率．
设函数f（x）＝
－sin（2x－
）．
（1）求函数f（x）的最大值和最小值；
（2）△ABC的内角A，B，C的对边分别为a，b，c，c＝3，f（
）＝
，若sinB＝2sinA，求△ABC的面积．