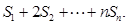如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,AE=1,CD与平面ABDE所成角的正弦值为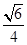 .
.
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D-EC-B的平面角的余弦值.
(本小题满分12分)已知函数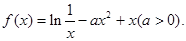
(1)若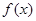 是单调函数,求
是单调函数,求 的取值范围;
的取值范围;
(2)若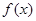 有两个极值点
有两个极值点 ,证明:
,证明:
(本小题满分12分)已知抛物线 的焦点为F,过点F作直线
的焦点为F,过点F作直线 与抛物线交于A,B两点,抛物线的准线与
与抛物线交于A,B两点,抛物线的准线与 轴交于点C。
轴交于点C。
(1)证明: ;
;
(2)求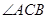 的最大值,并求
的最大值,并求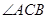 取得最大值时线段AB的长。
取得最大值时线段AB的长。
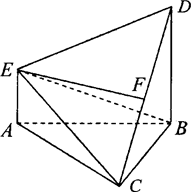
(本小题满分12分)如图,在四棱锥S—ABCD中,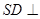 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且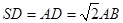 ,E是SA的中点。
,E是SA的中点。
(1)求证:平面BED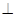 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小。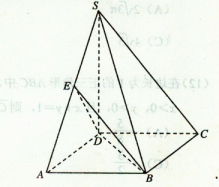
(本小题满分12分)张师傅驾车从公司开往火车站,途径4个交通岗,这4个交通岗将公司到火车站分成5个时段,每个时段的驾车时间都是3分钟,如果遇到红灯要停留1分钟。假设他在各交通岗遇到红灯是相互独立的,并且概率都是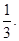
(1)求张师傅此行程时间不小于16分钟的概率;
(2)记张师傅此行程所需时间为Y分钟,求Y的分布列和均值。
(本小题满分12分)在等比数列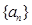 中,
中,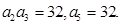
(1)求数列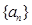 的通项公式;
的通项公式;
(2)设数列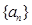 的前
的前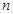 项和为
项和为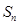 ,求
,求