(本小题满分7分) 选修4-4:坐标系与参数方程
平面直角坐标系中,直线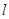 的参数方程是
的参数方程是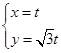 (
(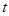 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,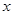 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线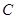 的极坐标方程为
的极坐标方程为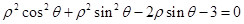 .
.
(Ⅰ)求直线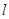 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线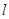 与曲线
与曲线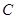 相交于
相交于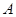 、
、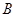 两点,求
两点,求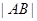 .
.
.(本小题满分12分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面(编号为①②③④⑤⑥)上安装5只颜色各异的灯,假若每只灯正常发光的概率为0.5,若一个侧面上至少有3只灯发光,则不需要更换这个面,否则需要更换这个面,假定更换一个面需要100元,用 表示更换的面数,用
表示更换的面数,用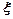 表示更换费用。
表示更换费用。
(1)求①号面需要更换的概率;
(2)求6个面中恰好有2个面需要更换的概率;
(3)写出 的分布
的分布 列,求
列,求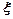 的数学期望。
的数学期望。
.(本小题满分12分)
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC的中点。
(1)证明:SO⊥平面ABC;
(2)求二面角A-SC-B的余弦值.
(本小题满分12分)
已知向量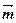 =(sin2x,cosx),
=(sin2x,cosx),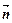 =(
=(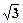 ,2cosx)(x∈R),f(x)=
,2cosx)(x∈R),f(x)=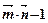
(1)求f(x)的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别为a,b,c,f(A)=2,a=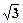 ,B=
,B=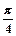 ,求b的值。
,求b的值。
( (本小题满分12分)
设椭圆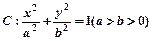 的离心率为
的离心率为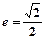 ,点
,点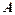 是椭圆上的一点,且点
是椭圆上的一点,且点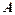 到椭圆
到椭圆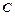 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆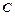 的方程;
的方程;
(2)椭圆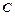 上一动点
上一动点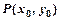 ,关于直线
,关于直线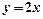 的对称点为
的对称点为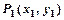 ,求
,求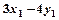 的取值范围.
的取值范围.
( (本小题满分12分)
设函数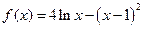 .
.
(Ⅰ)求函数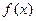 的单调递增区间;
的单调递增区间;
(Ⅱ)若关于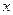 的方程
的方程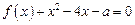 在区间
在区间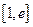
 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数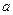 的取值范围.
的取值范围.