( (本小题满分12分)
设椭圆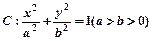 的离心率为
的离心率为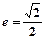 ,点
,点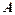 是椭圆上的一点,且点
是椭圆上的一点,且点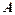 到椭圆
到椭圆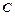 两焦点的距离之和为4.
两焦点的距离之和为4.
(1)求椭圆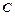 的方程;
的方程;
(2)椭圆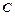 上一动点
上一动点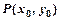 ,关于直线
,关于直线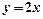 的对称点为
的对称点为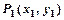 ,求
,求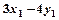 的取值范围.
的取值范围.
已知椭圆 的离心率
的离心率 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,过椭圆右焦点
的焦点重合,过椭圆右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于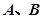 两点.
两点.
(1)求椭圆标准方程;
(2)设点 ,且
,且 ,求直线
,求直线 方程.
方程.
函数
(1) 时,求
时,求 最小值;
最小值;
(2)若 在
在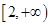 是单调增函数,求
是单调增函数,求 取值范围.
取值范围.
某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.
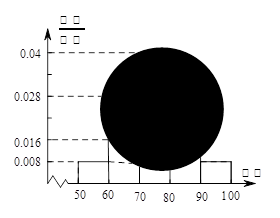
(1)求全班人数,并求出分数在 之间的频数;
之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中 间的矩形的高.
间的矩形的高.
某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对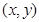 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”
号车站下车”
(1)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(2)求甲、乙两人同在第3号车站下车的概率;
(3)求甲、乙两人在不同的车站下车的概率.
(本小题满分14分)
已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)证明:对任意 恒成立;
恒成立;
(3)对于函数 图象上的不同两点
图象上的不同两点 ,如果在函数
,如果在函数 图象上存在点
图象上存在点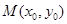 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称直线
,则称直线 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当 时,又称直线
时,又称直线 存在 “中值伴侣切线”.试问:当
存在 “中值伴侣切线”.试问:当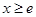 时,对于函数
时,对于函数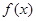 图象上不同两点
图象上不同两点 、
、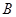 ,直线
,直线 是否存在“中值伴侣切线”?证明你的结论.
是否存在“中值伴侣切线”?证明你的结论.