(本小题满分14分)
已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)证明:对任意 恒成立;
恒成立;
(3)对于函数 图象上的不同两点
图象上的不同两点 ,如果在函数
,如果在函数 图象上存在点
图象上存在点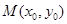 (其中
(其中 )使得点
)使得点 处的切线
处的切线 ,则称直线
,则称直线 存在“伴侣切线”.特别地,当
存在“伴侣切线”.特别地,当 时,又称直线
时,又称直线 存在 “中值伴侣切线”.试问:当
存在 “中值伴侣切线”.试问:当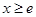 时,对于函数
时,对于函数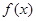 图象上不同两点
图象上不同两点 、
、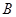 ,直线
,直线 是否存在“中值伴侣切线”?证明你的结论.
是否存在“中值伴侣切线”?证明你的结论.
一走廊拐角处的横截面如图所示,已知内壁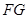 和外壁
和外壁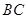 都是半径为1m的四分之一圆弧,
都是半径为1m的四分之一圆弧, 分别与圆弧
分别与圆弧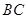 相切于
相切于 两点,
两点, 且两组平行墙壁间的走廊宽度都是1m.
且两组平行墙壁间的走廊宽度都是1m.
(1)若水平放置的木棒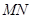 的两个端点
的两个端点 分别在外壁
分别在外壁 和
和 上,且木棒与内壁圆弧相切于点
上,且木棒与内壁圆弧相切于点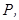 设
设 试用
试用 表示木棒
表示木棒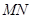 的长度
的长度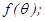
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.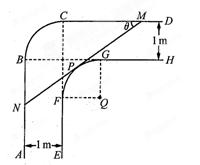
在 中,内角
中,内角 所对的边分别为
所对的边分别为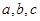 .已知
.已知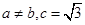 ,
,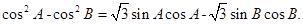
(1)求角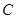 的大小;
的大小;
(2)若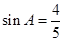 ,求
,求 的面积.
的面积.
已知命题 指数函数
指数函数 在
在 上单调递减,命题
上单调递减,命题 关于
关于 的方程
的方程
 的两个实根均大于3.若“
的两个实根均大于3.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知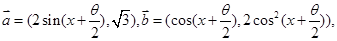 且
且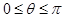 ,
,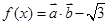 ,且
,且 为偶函数.
为偶函数.
(1)求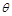 ;
;
(2)求满足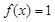 ,
, 的x的集合.
的x的集合.
设函数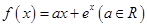
(1)若函数 有且只有两个零点
有且只有两个零点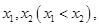 求实数
求实数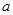 的取值范围;
的取值范围;
(2)当 时
时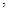 若曲线
若曲线 上存在横坐标成等差数列的三个点
上存在横坐标成等差数列的三个点
①证明: 为钝角三角形;
为钝角三角形;
②试判断 能否为等腰三角形
能否为等腰三角形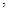 并说明理由
并说明理由