某市地铁全线共有四个车站,甲、乙两人同时在地铁第1号车站(首发站)乘车,假设每人自第2号站开始,在每个车站下车是等可能的,约定用有序实数对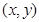 表示“甲在
表示“甲在 号车站下车,乙在
号车站下车,乙在 号车站下车”
号车站下车”
(1)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(2)求甲、乙两人同在第3号车站下车的概率;
(3)求甲、乙两人在不同的车站下车的概率.
有11名划船运动员,其中有5人会左浆,4人会右浆,还有甲、乙两人即会左浆,又会右浆,现要派出4名左浆手,4名右浆手,组成划船队,有多少种选派方案?
如图1-2-1所示,在某个城市中,M,N两地之间有整齐的道路网,若规定只能向东或向北两个方向沿图中路线前进,则从M到N不同的走法共有多少种?
甲、乙、丙、丁、戊5名同学手拉手站成一圈,有多少种不同的站法?
从6名运动员中选出4个参加4×100m接力赛,如果甲不跑第一棒,乙不跑第四棒,共有多少种不同的参赛方法?
从a,b,c,d,e这5个元素中取出4个放在4个不同的格子中,要求一个格子放一个元素,且元素b 不能放在第二个格子里,问共有多少种不同的放法?