（本题满分共12分）某流感病研究中心对温差与甲型H1N1病毒感染数之间的相关关系进行研究，他们每天将实验室放入数量相同的甲型H1N1病毒和100头猪，然后分别记录了4月1日至4月5日每天昼夜温差与实验室里100头猪的感染数，得到如下资料：
| 日 期 |
4月1日 |
4月2日 |
4月3日 |
4月4日 |
4月5日 |
| 温 差 |
10 |
13 |
11 |
12 |
7 |
| 感染数 |
23 |
32 |
24 |
29 |
17 |
（1）求这5天的平均感染数；（2）从4月1日至4月5日中任取2天，记感染数分别为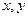
用
的形式列出所有的基本事件， 其中
视为同一事件,并求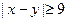
的事件A的概率。
}是首项为23,公差为整数的等差数列,且前6项为正,从第7项开始变为负的,回答下列各问：(1)求此等差数列的公差d;(2)设前n项和为
,求
求
的值。
，函数
（其中
，e是自然对数的底数）．
时，求函数
的极值；
在
上恒成立，求实数a的取值范围；
，求证：
（其中e是自然对数的底数）．