已知椭圆 的离心率
的离心率 ,它的一个焦点与抛物线
,它的一个焦点与抛物线 的焦点重合,过椭圆右焦点
的焦点重合,过椭圆右焦点 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线 ,交椭圆于
,交椭圆于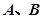 两点.
两点.
(1)求椭圆标准方程;
(2)设点 ,且
,且 ,求直线
,求直线 方程.
方程.
已知集合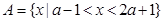 ,
, ,
,
(1)若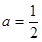 ,求
,求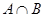 .
.
(2)若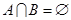 ,求实数a的取值范围.
,求实数a的取值范围.
已知全集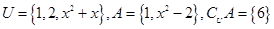 ,求实数
,求实数 的值.
的值.
(本小题满分12分)已知 其中
其中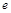 是自然对数的底 .
是自然对数的底 .
(1)若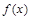 在
在 处取得极值,求
处取得极值,求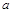 的值;
的值;
(2)求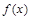 的单调区间;
的单调区间;
(3)设 ,存在
,存在 ,使得
,使得 成立,求
成立,求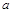 的取值范围.
的取值范围.
(本小题满分12分)函数f(x)=loga(x2-4ax+3a2), 0<a<1, 当x∈[a+2,a+3]时,恒有|f(x)|≤1,试确定a的取值范围.
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重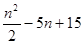 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为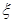 ,求E
,求E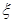 .
.