.(本小题满分12分)
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC的中点。
(1)证明:SO⊥平面ABC;
(2)求二面角A-SC-B的余弦值.
(本小题满分12分)如图1,在直角梯形 中,
中,
 ,
,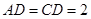 ,点
,点 为线段
为线段 的中点,将
的中点,将 沿
沿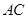 折起,使平面
折起,使平面 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.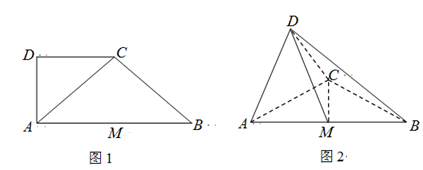
(Ⅰ)求证: 平面
平面 ;
;
【理】(Ⅱ)求二面角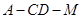 的余弦值.
的余弦值.
【文】(Ⅱ)求点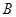 到平面
到平面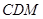 的距离.
的距离.
(本小题满分12分)已知圆 经过
经过 、
、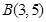 两点,且圆心
两点,且圆心 在直线
在直线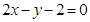 上.
上.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)若直线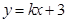 与圆
与圆 总有公共点,求实数
总有公共点,求实数 的取值范围.
的取值范围.
(本小题满分10分)已知命题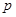 :
: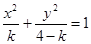 表示焦点在
表示焦点在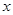 轴上的椭圆,命题
轴上的椭圆,命题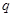 :
: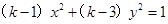 表示双曲线.若
表示双曲线.若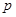 或
或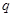 为真,
为真,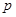 且
且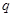 为假,求
为假,求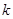 的取值范围.
的取值范围.
已知抛物线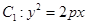 与椭圆
与椭圆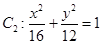 在第一象限的交点为B,O为坐标原点,A是椭圆右顶点,
在第一象限的交点为B,O为坐标原点,A是椭圆右顶点,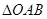 的面积为
的面积为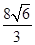 .
.
(1)求抛物线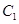 的方程;
的方程;
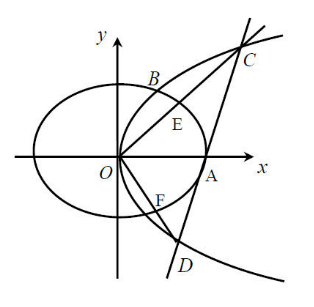
(2)过A点作直线 交
交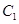 于C,D两点,射线OC,OD分别交
于C,D两点,射线OC,OD分别交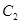 于E,F两点,记
于E,F两点,记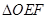 和
和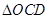 的面积分别为
的面积分别为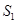 和
和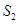 ,问是否存在直线
,问是否存在直线 ,使得
,使得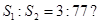 若存在,求出直线
若存在,求出直线 方程,若不存在,请说明理由.
方程,若不存在,请说明理由.
已知抛物线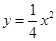 ,圆
,圆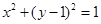 ,过点
,过点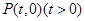 作不过原点O的直线PA,PB分别与抛物线和圆相切,A,B为切点(A为抛物线切点,B为圆的切点).
作不过原点O的直线PA,PB分别与抛物线和圆相切,A,B为切点(A为抛物线切点,B为圆的切点).
(1)求点A,B坐标;
(2)求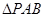 面积.
面积.