(本小题满分14分)已知函数 (
(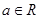 且
且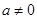 ),
),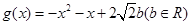 .
.
(Ⅰ)若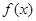 在定义域上有极值,求实数
在定义域上有极值,求实数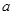 的取值范围;
的取值范围;
(Ⅱ)当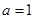 时,若对
时,若对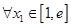 ,总
,总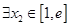 ,使得
,使得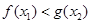 ,求实数
,求实数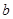 的取值范围;(其中
的取值范围;(其中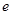 为自然对数的底数);
为自然对数的底数);
(Ⅲ)对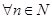 ,且
,且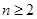 ,证明:
,证明: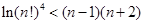 .
.
已知函数 ,
, .
.
(1)求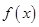 的最小正周期;
的最小正周期;
(2)求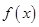 在
在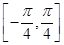 上的最小值和最大值.
上的最小值和最大值.
已知函数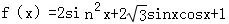 .
.
(1)求f(x)的最小正周期;
(2)求f(x)的单调递增区间;
(3)求f(x)在 上的最值及取最值时x的值.
上的最值及取最值时x的值.
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
(2)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率.
已知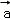 ,
,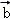 ,
,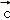 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中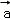 =(1,2)
=(1,2)
(1)若|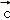 |=2
|=2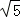 ,
,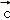 ∥
∥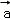 ,求
,求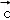 的坐标及
的坐标及 ;
;
(2)若|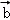 |=
|=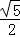 ,且
,且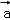 +2
+2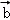 与3
与3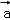 ﹣
﹣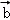 垂直,求
垂直,求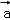 与
与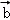 的夹角.
的夹角.
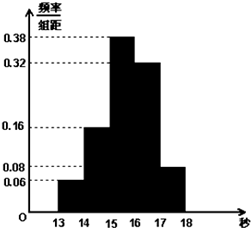
某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计学校900名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数.