(本小题满分7分)选修4-2:矩阵与变换
二阶矩阵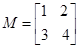 ;
;
(Ⅰ)求点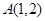 在变换
在变换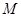 作用下得到的点
作用下得到的点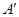 ;
;
(Ⅱ)设直线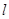 在变换
在变换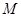 作用下得到了直线
作用下得到了直线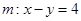 ,求点
,求点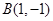 到直线
到直线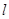 的距离.
的距离.
(本小题满分12分)
如图1,矩形ABCD中,AB=2AD=2a,E为DC的中点,现将△ADE沿AE折起,使平面ADE⊥平面ABCE,如图2.(I)求二面角A—BC—D的正切值;
|
(Ⅱ)求证:AD⊥平面BDE.
(本小题满分12分)向量a=(sinωx+cosωx,1),b=(f(x),simωx),其中0<ω<l,且a∥b.将f(x)的图象沿x轴向左平移 个单位,沿y轴向下平移
个单位,沿y轴向下平移 个单位,得到g(x)的图象,已知g(x)的图象关于(
个单位,得到g(x)的图象,已知g(x)的图象关于( ,0)对称(I)求ω的值; (Ⅱ)求g(x)在[0,4π]上的单调递增区间.
,0)对称(I)求ω的值; (Ⅱ)求g(x)在[0,4π]上的单调递增区间.
(本小题满分12分)
已知集合 ;命题p:x ∈ A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.
;命题p:x ∈ A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.
已知函数 图象上一点
图象上一点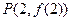 处的切线方程为
处的切线方程为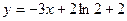 .
.
(Ⅰ)求 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求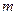 的取值范围(其中
的取值范围(其中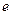 为自然对数的底数,
为自然对数的底数,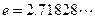 );
);
等比数列{ }的前n 项和为
}的前n 项和为 ,已知
,已知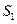 ,
,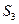 ,
, 成等差数列(1)求{
成等差数列(1)求{ }的公比q;(2)求
}的公比q;(2)求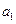 -
- =3,求
=3,求