已知椭圆长轴的左右端点分别为A，B，短轴的上端点为M，O为椭-优题课

题文

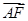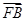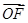已知椭圆长轴的左右端点分别为A，B，短轴的上端点为M，O为椭圆的中心，F为椭圆的右焦点，且·＝1，｜｜＝1．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若直线l交椭圆于P，Q两点，问：是否存在直线l，使得点F恰为△PQM的垂心?若存在，求出直线l的方程；若不存在，请说明理由．

科目数学题型解答题难度较难

登录免费查看答案和解析

相关试题

已知函数f(t)= $f (t) = \sqrt{\frac{1 - t}{1 + t}}$ , $g (x) = c o s x \cdot f (s i n x) + s i n x \cdot f (c o s x)$ , $x \in (π, \frac{17 π}{12})$ .

（Ⅰ）将函数 $g (x)$ 化简成 $A \sin (ω x + φ) + B （ A ＞ 0 ， ω ＞ 0 ， φ \in [0 ， 2 π] ）$ 的形式；
（Ⅱ）求函数 $g (x)$ 的值域。

已知以 $a_{1}$ 为首项的数列 $\{a_{n}\}$ 满足：
（1）当 $a_{1} ＝ 1$ ， $c ＝ 1$ ， $d ＝ 3$ 时，求数列 $\{a_{n}\}$ 的通项公式；
（2）当 $0 ＜ a_{1} ＜ 1$ ， $c ＝ 1$ ， $d ＝ 3$ 时，试用 $a_{1}$ 表示数列 $\{a_{n}\}$ 的前 $100$ 项的和 $S_{100}$ ；
（3）当 $0 ＜ a_{1} ＜ m$ （ $m$ 是正整数）， $c ＝ 1$ ， $d \geq 3 m$ 时，求证：数列 $a_{2}$ ， $a_{3 m + 2}$ ， $a_{6 m + 2}$ ， $a_{9 m + 2}$ 成等比数列当且仅当 $d ＝ 3 m$ .

设 $P (a, b) (b \neq 0)$ 是平面直角坐标系 $x O y$ 中的点， $l$ 是经过原点与点 $(1, b)$ 的直线，记 $Q$ 是直线 $l$ 与抛物线 $x^{2} = 2 p y (p \neq 0)$ 的异于原点的交点
（1）若 $a = 1, b = 2, p = 2$ ，求点 $Q$ 的坐标；
（2）若点 $P (a, b) (a b \neq 0)$ 在椭圆 $\frac{x^{2}}{4} + y^{2} = 1$ 上， $p = \frac{1}{2 a b}$ ，求证：点 $Q$ 落在双曲线 $4 x^{2} - 4 y^{2} = 1$ 上；
（3）若动点 $P (a, b)$ 满足 $a b \neq 0$ ， $p = \frac{1}{2 a b}$ ，若点 $Q$ 始终落在一条关于 $x$ 轴对称的抛物线上，试问动点 $P$ 的轨迹落在哪种二次曲线上，并说明理由.

已知函数 $f (x) = 2^{x} - \frac{1}{2^{x}}$ .
（1）若 $f (x) = 2$ ，求 $x$ 的值；
（2）若 $2^{t} f (2 t) + m f (t) \geq 0$ 对于 $t \in [1, 2]$ 恒成立，求实数 $m$ 的取值范围.

已知双曲线 $C : \frac{x^{2}}{4} - y^{2} = 1$ ， $P$ 为 $C$ 上的任意点.
（1）求证：点 $P$ 到双曲线 $C$ 的两条渐近线的距离的乘积是一个常数；
（2）设点 $A$ 的坐标为 $(3, 0)$ ，求 $|P A|$ 的最小值.

试卷网试题网古诗词网作文网范文网