已知A、B、C是三角形ABC的三内角,且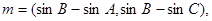
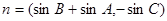 ,并且
,并且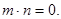
(1)求角A的大小。
(2)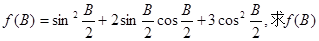 的递增区间。
的递增区间。
已知函数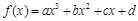 为奇函数,且在
为奇函数,且在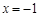 处取得极大值2.
处取得极大值2.
(Ⅰ)求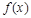 的解析式;
的解析式;
(Ⅱ)过点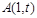 (
(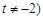 可作函数
可作函数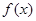 图像的三条切线,求实数
图像的三条切线,求实数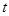 的取值范围;
的取值范围;
(Ⅲ)若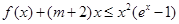 对于任意的
对于任意的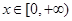 恒成立,求实数
恒成立,求实数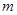 的取值范围.
的取值范围.
已知直线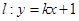 过定点
过定点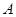 ,动点
,动点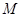 满足
满足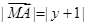 ,动点
,动点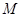 的轨迹为
的轨迹为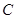 .
.
(Ⅰ)求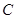 的方程;
的方程;
(Ⅱ)直线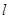 与
与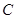 交于
交于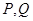 两点,以
两点,以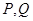 为切点分别作
为切点分别作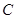 的切线,两切线交于点
的切线,两切线交于点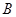 .
.
①求证: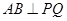 ;②若直线
;②若直线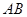 与
与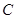 交于
交于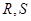 两点,求四边形
两点,求四边形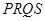 面积的最大值.
面积的最大值.
在数列 中,
中,
(Ⅰ)求数列 的前
的前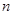 项和
项和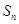 ;
;
(Ⅱ)若存在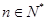 ,使得
,使得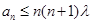 成立,求实数
成立,求实数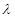 的最小值.
的最小值.
如图1,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CAB=45o,F为 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图2).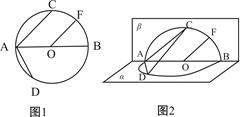
(Ⅰ)求证:OF//平面ACD;
(Ⅱ)在 上是否存在点
上是否存在点 ,使得平面
,使得平面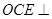 平面ACD?若存在,试指出点
平面ACD?若存在,试指出点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.