如图,设正三棱锥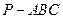 的侧棱长为
的侧棱长为 ,
,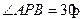 ,
, ,
,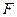 分别是
分别是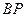 ,
,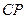 上的点,求
上的点,求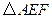 周长的最小值.
周长的最小值.
 |
一自来水厂用蓄水池通过管道向所管辖区域供水.某日凌晨,已知蓄水池有水9千吨,水厂计划在当日每小时向蓄水池注入水2千吨,且每 小时通过管道向所管辖区域供水
小时通过管道向所管辖区域供水 千吨.
千吨.
(1)多少小时后,蓄水池存水量最少?
(2)当蓄水池存水量少于3千吨时,供水就会出现紧张现象,那么当日出现这种情况的时间有多长?
已知函数 ,
, .
.
(1)设 是函数
是函数 的一个零点,求
的一个零点,求 的值;
的值;
(2)求函数 的单调递增区间.
的单调递增区间.
如图,在正四棱锥 中,
中, .
.
(1)求该正四棱锥的体积 ;
;
(2)设 为侧棱
为侧棱 的中点,求异面直线
的中点,求异面直线 与
与
所成角 的大小.
的大小.
设点 是抛物线
是抛物线

 的焦点,
的焦点, 是抛物线
是抛物线 上的
上的 个不同的点(
个不同的点(
 ).
).
(1) 当 时,试写出抛物线
时,试写出抛物线 上的三个定点
上的三个定点 、
、 、
、 的坐标,从而使得
的坐标,从而使得 ;
;
(2)当 时,若
时,若 ,
,
求证: ;
;
(3) 当 时,某同学对(2)的逆命题,即:
时,某同学对(2)的逆命题,即:
“若 ,则
,则 .”
.”
开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
① 试构造一个说明该逆命题确实是假命题的反例(本研究方向最高得4分);
② 对任意给定的大于3的正整数 ,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
,试构造该假命题反例的一般形式,并说明你的理由(本研究方向最高得8分);
③ 如果补充一个条件后能使该逆命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由(本研究方向最高得10分).
【评分说明】本小题若填空不止一个研究方向,则以实得分最高的一个研究方向的得分作为本小题的最终得分.
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1)求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2)若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.