已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)
已知等比数列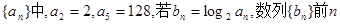 项的和为
项的和为 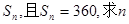 的值。
的值。
(本小题满分12分)
在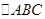 中,角
中,角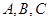 所对的边分别为
所对的边分别为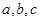 且满足
且满足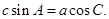
(I)求角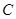 的大小;
的大小;
(II)求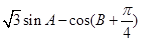 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角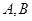 的大小.
的大小.
(本小题满分10分)
已知函数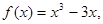
(1)求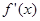 ;
;
(2)求过点A(0,16)的曲线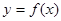 的切线方程。
的切线方程。
(本小题满分12分)已知椭圆的中心在坐标原点O,长轴长为2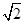 ,离心率e=
,离心率e=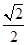 ,过右焦点F的直线l交椭圆于P、Q两点.
,过右焦点F的直线l交椭圆于P、Q两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若OP、OQ为邻边的平行四边形是矩形,求满足该条件的直线l的方程.
(本小题满分12分)设递增等比数列{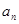 }的前n项和为
}的前n项和为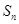 ,且
,且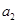 =3,
=3,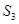 =13,数列{
=13,数列{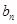 }满足
}满足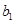 =
=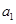 ,点P(
,点P(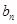 ,
,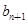 )在直线x-y+2=0上,n∈N﹡.
)在直线x-y+2=0上,n∈N﹡.
(Ⅰ)求数列{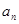 },{
},{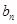 }的通项公式;
}的通项公式;
(Ⅱ)设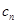 =
=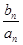 ,数列{
,数列{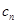 }的前n项和
}的前n项和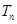 ,若
,若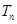 >2a-1恒成立(n∈N﹡),求实数a的取值范围.
>2a-1恒成立(n∈N﹡),求实数a的取值范围.