一自来水厂用蓄水池通过管道向所管辖区域供水.某日凌晨,已知蓄水池有水9千吨,水厂计划在当日每小时向蓄水池注入水2千吨,且每 小时通过管道向所管辖区域供水
小时通过管道向所管辖区域供水 千吨.
千吨.
(1)多少小时后,蓄水池存水量最少?
(2)当蓄水池存水量少于3千吨时,供水就会出现紧张现象,那么当日出现这种情况的时间有多长?
(本小题满分12分)
已知数列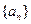 为递减的等差数列,
为递减的等差数列,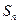 是数列
是数列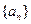 的前
的前 项和,且
项和,且 .
.
⑴ 求数列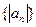 的前
的前 项和
项和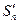 ;
;
⑵ 令 ,求数列
,求数列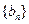 的前
的前 项和
项和 .
.
(本小题满 分12分)
分12分)
已知函数 ,
,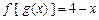 .(1)求
.(1)求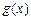 的解析式;(2) 求
的解析式;(2) 求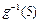 的值.
的值.
已知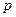 :
: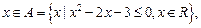
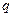 :
: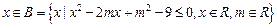 (1)若
(1)若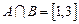 ,求实数
,求实数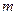 的值;
的值;
(2)若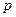 是
是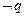 的充分条件,求实数
的充分条件,求实数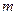 的取值范围.
的取值范围.
(本小题满分14分)
已知函数f(x)的定义域为 ,
, 且同时满足:①f(1)=3;②
且同时满足:①f(1)=3;②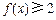 对一切
对一切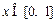 恒成立;③若
恒成立;③若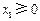 ,
, ,
,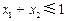 ,则
,则 .
.
①求函数f(x)的最大值 和最小值;
和最小值;
②试比较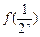 与
与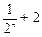
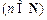 的大小;
的大小;
③某同学发现:当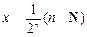 时,有
时,有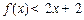 ,由此他提出猜想:对一切
,由此他提出猜想:对一切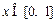 ,都有
,都有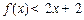 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
(本小题满分14分)
设函数 是定义域在R上的奇函数.
是定义域在R上的奇函数.
(1)若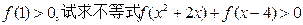 的解集;
的解集;
(2)若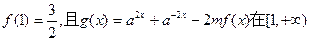 上的最小值为—2,求m的值.
上的最小值为—2,求m的值.