已知函数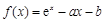 (
(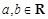 ),且函数图象过原点.
),且函数图象过原点.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)函数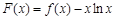 在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若 ,当
,当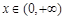 时,不等式
时,不等式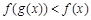 恒成立,求a的取值范围.
恒成立,求a的取值范围.
如图,已知椭圆Γ: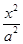 +
+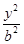 =1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足|
=1(a>b>0)的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的一个动点,满足|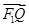 |=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足
|=2a.点P是线段F1Q与该椭圆的交点,点M在线段F2Q上,且满足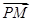 ·
·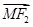 =0,|
=0,|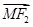 |≠0.
|≠0.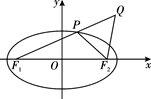
(Ⅰ)求点M的轨迹C的方程;
(Ⅱ)设不过原点O的直线l与轨迹C交于A,B两点,若直线OA,AB,OB的斜率依次成等比数列,求△OAB面积的取值范围;
(Ⅲ)由(Ⅱ)求解的结果,试对椭圆Γ写出类似的命题.(只需写出类似的命题,不必说明理由)
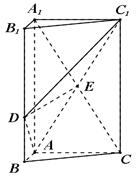
如图,三棱柱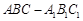 中,
中,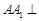 平面
平面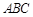 ,
,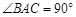 ,
,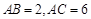 , 点
, 点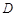 在线段
在线段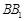 上,且
上,且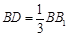 ,
,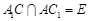 .
.
(Ⅰ)求证:直线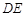 与平面
与平面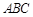 不平行;
不平行;
(Ⅱ)设平面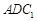 与平面
与平面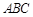 所成的锐二面角为
所成的锐二面角为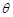 ,若
,若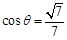 ,求
,求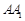 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面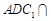 平面
平面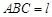 ,求直线
,求直线 与
与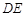 所成的角的余弦值.
所成的角的余弦值.
在2014年全国超级联赛上,兵乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲,乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
| 出场顺序 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 获胜概率 |
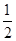 |
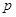 |
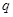 |
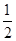 |
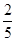 |
若甲队横扫对手获胜(即3:0获胜)的概率是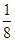 ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为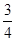
(Ⅰ)求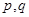 的值
的值
(Ⅱ)求甲队获胜场数的分布列和数学期望
凸四边形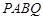 中,其中
中,其中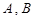 为定点,
为定点,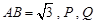 为动点,满足
为动点,满足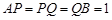 .
.
(1)写出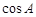 与
与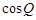 的关系式;
的关系式;
(2)设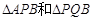 的面积分别为
的面积分别为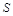 和
和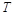 ,求
,求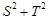 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形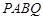 的面积.
的面积.