在一个平面上,机器人到与点 距离为
距离为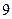 的地方绕
的地方绕 点顺时针而行,在行进过程中保持与点
点顺时针而行,在行进过程中保持与点 的距离不变.它在行进过程中到经过点
的距离不变.它在行进过程中到经过点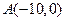 与
与 的直线的最近距离和最远距离分别是多少?
的直线的最近距离和最远距离分别是多少?
(本小题满分12分)(解答过程写在试卷上无效)
已知函数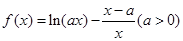
(1)求函数 的最值;
的最值;
(2)当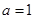 时,是否存在过点
时,是否存在过点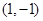 的直线与函数
的直线与函数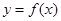 的图像相切?若存在,有多少条?若不存在,说明理由.
的图像相切?若存在,有多少条?若不存在,说明理由.
(本小题满分12分)(解答过程写在试卷上无效)
对于函数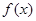 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称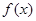 为“局部奇函数”.
为“局部奇函数”. 为定义在
为定义在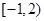 上的“局部奇函数”;
上的“局部奇函数”;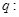 曲线
曲线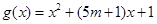 与
与 轴交于不同的两点;
轴交于不同的两点;
若 为假命题,
为假命题,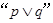 为真命题,求
为真命题,求 的取值范围.
的取值范围.
(本小题满分10分)选修4-5:不等式选讲
已知函数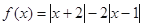
(1)解不等式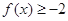 ;
;
(2)对任意 ,都有
,都有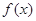
 成立,求实数
成立,求实数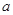 的取值范围.
的取值范围.
(本小题满分14分)已知函数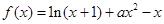 (
(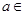 R).
R).
(1)当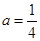 时,求函数
时,求函数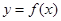 的单调区间;
的单调区间;
(2)若对任意实数 ,当
,当 时,函数
时,函数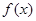 的最大值为
的最大值为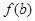 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有 升水,桶2是空的,
升水,桶2是空的, 分钟后桶1中剩余的水量符合指数衰减曲线
分钟后桶1中剩余的水量符合指数衰减曲线 (其中
(其中 是常数,
是常数, 是自然对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
是自然对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(1)桶2中的水 (升)与时间
(升)与时间 (分钟)的函数关系式;
(分钟)的函数关系式;
(2)再过多少分钟,桶1中的水是 升?
升?