已知直线 与
与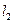 的方程分别为
的方程分别为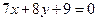 ,
,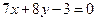 ,直线
,直线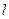 平行于
平行于 ,直线
,直线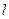 与
与 ,
,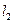 的距离分别为
的距离分别为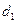 ,
,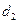 ,且
,且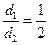 ,求直线
,求直线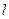 的方程.
的方程.
如图,在底面是正方形的四棱锥P—ABCD中,平面PCD⊥平面ABCD,PC=PD=CD=2.
(I)求证:PD⊥BC;
(II)求二面角B—PD—C的正切值。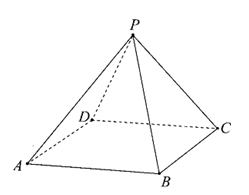
在△ABC中,角A、B、C的对边分别为a、b、c,向量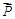 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
=
(Ⅰ)求角B的大小;
(Ⅱ)设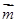 =(sin(C+
=(sin(C+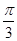 ),
),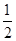 ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
已知函数 (
(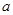 为实数).
为实数).
(Ⅰ)当 时,求
时,求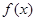 的最小值;
的最小值;
(Ⅱ)若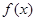 在
在 上是单调函数,求
上是单调函数,求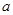 的取值范围.
的取值范围.
设 的导数为
的导数为 ,若函数
,若函数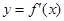 的图象关于直线
的图象关于直线 对称,且
对称,且 .
.
(Ⅰ)求实数 ,
, 的值;
的值;
(Ⅱ)求函数 的单调区间.
的单调区间.
已知函数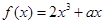 的图象经过点
的图象经过点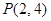 .
.
(Ⅰ)求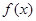 的表达式及其导数
的表达式及其导数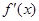 ;
;
(Ⅱ)求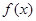 在闭区间
在闭区间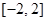 上的最大值和最小值.
上的最大值和最小值.