(本小题满分16分)已知函数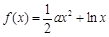 ,
,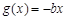 ,设
,设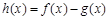 .
.
(1)若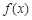 在
在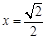 处取得极值,且
处取得极值,且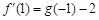 ,求函数h(x)的单调区间;
,求函数h(x)的单调区间;
(2)若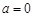 时函数h(x)有两个不同的零点x1,x2.
时函数h(x)有两个不同的零点x1,x2.
①求b的取值范围;②求证: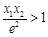 .
.
重庆市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB =" AD" = 4万米,BC = 6万米,CD = 2万米,
(1)请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值;
(2)因地理条件的限制,边界AD、DC不能变更,而边界AB、BC可以调整,为了提高棚户区改造建筑用地的利用率,请在圆弧ABC上设计一点P,使得棚户区改造的新建筑用地APCD的面积最大,并求最大值.
已知函数 的定义域是(0,
的定义域是(0, ),当x > 1时,
),当x > 1时, >0,且
>0,且 ,
,
(1)证明: 在定义域上是增函数;
在定义域上是增函数;
(2)若 ,解不等式
,解不等式 .
.
已知向量 =(
=( ,
, ),
), =(
=( ,
, ),设
),设 ,
,
(1)求 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)若 ,求
,求 的值域;
的值域;
(3)若 的图象按
的图象按 =(t,0)作长度最短的平移后,其图象关于原点对称,求
=(t,0)作长度最短的平移后,其图象关于原点对称,求 的坐标.
的坐标.
设函数 ,且关于x的不等式
,且关于x的不等式 的解集为
的解集为 ,
,
(1)求b的值;
(2)解关于x的不等式 (
( ).
).
已知 ,
, ,且
,且 ,
, ,
,
(1)求 ,
, ;
;
(2)求( )与
)与 的夹角.
的夹角.