某食品厂每天需用食品配料200千克,配料的价格为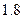 元/千克,每次进货需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.(Ⅰ)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?
元/千克,每次进货需支付运费236元.每次购买来的配料还需支付保管费用,其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.(Ⅰ)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?
(Ⅱ)设该厂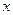 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这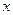 天中用于配料的总费用
天中用于配料的总费用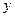 (元)关于
(元)关于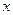 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
已知等差数列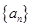 的首项
的首项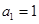 ,公差
,公差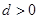 ,且其第二项、第五项、第十四项分别是等比数列
,且其第二项、第五项、第十四项分别是等比数列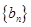 的第二、三、四项.
的第二、三、四项.
(1)求数列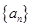 与
与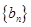 的通项公式;
的通项公式;
(2)令数列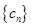 满足:
满足: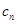 =
= ,求数列
,求数列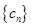 的前101项之和
的前101项之和 ;
;
(3)设数列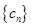 对任意
对任意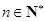 ,均有
,均有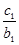 +
+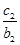 + +
+ +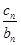 =
= 成立,求
成立,求 的值.
的值.
如图,边长为2的正方形 所在的平面与平面
所在的平面与平面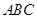 垂直,
垂直,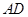 与
与 的交点为
的交点为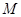 ,
, 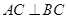 ,且
,且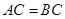 .
.
(1)求证: 平面
平面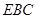 ;
;
(2)求直线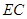 与平面
与平面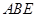 所成线面角的正切值.
所成线面角的正切值.
在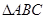 中,角
中,角 为锐角,已知内角
为锐角,已知内角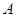 、
、 、
、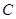 所对的边分别为
所对的边分别为 、
、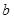 、
、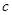 ,向量
,向量 且向量
且向量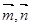 共线.
共线.
(1)求角 的大小;
的大小;
(2)如果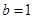 ,且
,且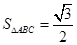 ,求
,求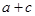 的值.
的值.
设向量
(1)若 ;
;
(2)设函数 的最大值.
的最大值.
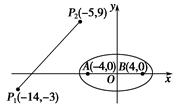
为了考察冰川的融化状况,一支科考队在某冰川上相距8 km的A,B两点各建一个考察基地.视冰川面为平面形,以过A,B两点的直线为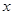 轴,线段AB的垂直平分线为
轴,线段AB的垂直平分线为 轴建立平面直角坐标系(如图).考察范围为到A,B两点的距离之和不超过10 km的区域.
轴建立平面直角坐标系(如图).考察范围为到A,B两点的距离之和不超过10 km的区域.
(1)求考察区域边界曲线的方程;
(2)如图所示,设线段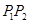 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2 km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2 km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?