已知实数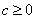 ,曲线
,曲线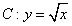 与直线
与直线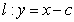 的交点为
的交点为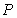 (异于原点
(异于原点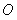 ),在曲线
),在曲线 上取一点
上取一点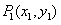 ,过点
,过点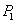 作
作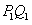 平行于
平行于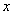 轴,交直线
轴,交直线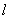 于点
于点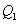 ,过点
,过点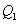 作
作 平行于
平行于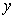 轴,交曲线
轴,交曲线 于点
于点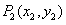 ,接着过点
,接着过点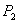 作
作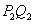 平行于
平行于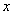 轴,交直线
轴,交直线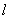 于点
于点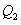 ,过点
,过点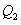 作
作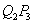 平行于
平行于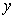 轴,交曲线
轴,交曲线 于点
于点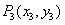 ,如此下去,可以得到点
,如此下去,可以得到点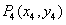 ,
,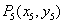 ,…,
,…,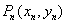 ,… . 设点
,… . 设点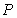 的坐标为
的坐标为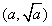 ,
,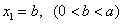 .
.
(Ⅰ)试用 表示
表示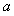 ,并证明
,并证明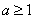 ;
;
(Ⅱ)试证明 ,且
,且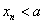 (
(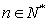 );
);
(Ⅲ)当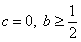 时,求证:
时,求证: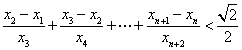 (
(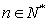 ).
).
已知 ,且
,且 为第三象限角,
为第三象限角,
(1)求 的值;
的值;
(2)求 的值。
的值。
已知中心在原点的双曲线的渐近线方程是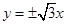 ,且双曲线过点
,且双曲线过点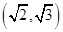
(Ⅰ)求双曲线的方程;
(Ⅱ)过双曲线右焦点 作倾斜角为
作倾斜角为 的直线交双曲线于
的直线交双曲线于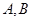 ,求
,求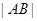 .
.
已知椭圆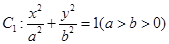 过点
过点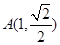 ,其焦距为
,其焦距为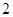 .
.
(Ⅰ)求椭圆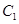 的方程;
的方程;
(Ⅱ)已知椭圆具有如下性质:若椭圆的方程为 ,则椭圆在其上一点
,则椭圆在其上一点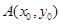 处
处
的切线方程为 ,试运用该性质解决以下问题:
,试运用该性质解决以下问题:
(i)如图(1),点 为
为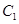 在第一象限中的任意一点,过
在第一象限中的任意一点,过 作
作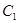 的切线
的切线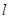 ,
,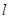 分别与
分别与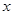 轴和
轴和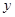 轴的正
轴的正
半轴交于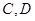 两点,求
两点,求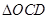 面积的最小值;
面积的最小值;
(ii)如图(2),过椭圆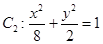 上任意一点
上任意一点 作
作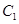 的两条切线
的两条切线 和
和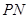 ,切点分别为
,切点分别为 .当点
.当点 在椭圆
在椭圆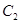 上运动时,是否存在定圆恒与直线
上运动时,是否存在定圆恒与直线 相切?若存在,求出圆的方程;
相切?若存在,求出圆的方程;
若不存在,请说明理由.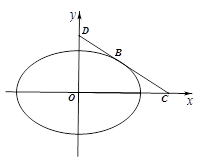
已知椭圆的一个顶点为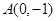 ,焦点在
,焦点在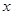 轴上,若右焦点到直线
轴上,若右焦点到直线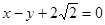 的距离为
的距离为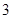 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在斜率为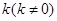 ,且过定点
,且过定点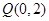 的直线
的直线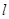 ,使
,使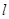 与椭圆交于两个不同的点
与椭圆交于两个不同的点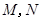 ,且
,且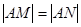 ?若存在,求出直线
?若存在,求出直线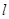 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
如图,抛物线关于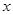 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点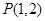 ,
,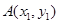 ,
,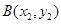 均在抛物线上.
均在抛物线上.
(Ⅰ)写出该抛物线的方程及其准线方程;
(Ⅱ)当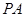 与
与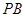 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求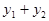 的值及直线
的值及直线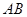 的斜率.
的斜率.