向量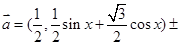 ,
,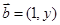 ,已知
,已知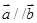 ,且有函数
,且有函数 .
.
(1)求函数 的周期;
的周期;
(2)已知锐角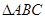 的三个内角分别为
的三个内角分别为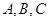 ,若有
,若有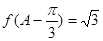 ,边
,边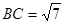 ,
,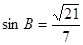 ,求
,求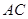 的长及
的长及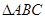 的面积.
的面积.
如右下图,在长方体ABCD—A1B1C1D1中,已知AB=" 4," AD ="3," AA1= 2。 E、F分别是线段AB、BC上的点,且EB= FB=1.
(1) 求二面角C—DE—C1的余弦值;
(2) 求直线EC1与FD1所成的余弦值.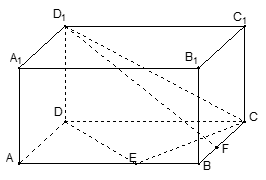
在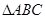 中,
中,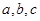 分别是角
分别是角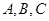 的对边,
的对边,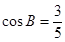 且
且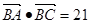
|
(Ⅰ)求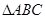 的面积;(Ⅱ)若
的面积;(Ⅱ)若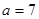 ,求角
,求角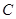 。
。
已知平面直角坐标系中点F(1,0)和直线 ,动圆M过点F且与直线
,动圆M过点F且与直线 相切。
相切。
(1)求M的轨迹L的方程;
(2)过点F作斜率为1的直线 交曲线L于A、B两点,求|AB|的值。
交曲线L于A、B两点,求|AB|的值。
已知:集合M是满足下列性质的函数f(x)的全体:在定义域内存在x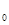 ,使得
,使得
f(x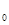 +1)=f(x
+1)=f(x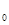 )+f(1)成立。
)+f(1)成立。
(1)函数f(x)= 是否属于集合M?说明理由;
是否属于集合M?说明理由;
(2)设函数f(x)=lg ,求实数a的取值范围;
,求实数a的取值范围;
(3)证明:函数f(x)=2 +x
+x
 M。
M。
已知:函数f(x)=ax(0<a<1),
(Ⅰ)若f(x )=2,求f(3x
)=2,求f(3x );
);
(Ⅱ)若f(2x -3x+1)
-3x+1) f(x
f(x +2x-5),求x的取值范围。
+2x-5),求x的取值范围。