已知多面体ABCDFE中, 四边形ABCD为矩形,AB∥EF,AF⊥BF,平面ABEF⊥平面ABCD, O、M分别为AB、FC的中点,且AB = 2,AD =" EF" = 1.
(Ⅰ)求证:AF⊥平面FBC;
(Ⅱ)求证:OM∥平面DAF;
(Ⅲ)设平面CBF将几何体EFABCD分成的两个锥体的体积分别为VF-ABCD,VF-CBE,求VF-ABCD∶VF-CBE 的值.
设全集 .
.
(1)解关于x的不等式 ;
;
(2)记A为(1)中不等式的解集,集合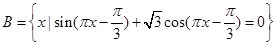 ,若
,若 恰有3个元素,求
恰有3个元素,求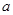 的取值范围.
的取值范围.
已知曲线C的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是 (t是参数)
(t是参数)
(1)将曲线C的极坐标方程和直线L参数方程转化为普通方程;
(2)若直线L与曲线C相交于M、N两点,且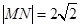 ,求实数m的值.
,求实数m的值.
如图⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于点N,过点N的切线交CA的延长线于P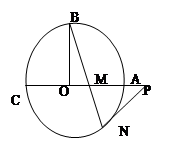
(1)求证:
(2)若⊙O的半径为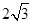 ,OA=
,OA= OM,求MN的长
OM,求MN的长
已知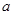 是实数,函数
是实数,函数 .
.
(1)若 ,求
,求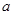 的值及曲线
的值及曲线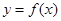 在点
在点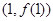 处的切线方程.
处的切线方程.
(2)求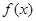 在
在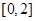 上的最大值.
上的最大值.
已知圆G: 经过椭圆
经过椭圆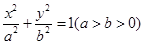 的右焦点F及上顶点B,过椭圆外一点(m,0)(
的右焦点F及上顶点B,过椭圆外一点(m,0)( )倾斜角为
)倾斜角为 的直线L交椭圆与C、D两点.
的直线L交椭圆与C、D两点.
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的内部,求m的取值范围.