一个质量为m的带正电荷的小球,栓在一根长为L的绝缘轻绳上,绳的另一个端固定在O点,小球位于水平向右的匀强电场中,平衡时细绳与竖直方向成α角,如图所示,现在用力使小球移到O点的竖直下方,绳被拉直,从静止释放小球,求它回到平衡位置时绳的拉力多大?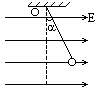
如图12-4-19所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN。导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=5Ω的电阻。有一匀强磁场垂直于导轨平面,磁感强度为B0=1T。将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好,导轨与金属棒的电阻均不计。现由静止释放金属棒,金属棒沿导轨向下运动过程中始终与NQ平行。已知金属棒与导轨间的动摩擦因数μ=0.5,当金属棒滑行至cd处时已经达到稳定速度,cd距离NQ为s=1m。试解答以下问题:(g=10m/s2,sin37°=0.6,cos37°=0.8)
(1)请定性说明金属棒在达到稳定速度前的加速度和速度各如何变化?(2)当金属棒滑行至cd处时回路中的电流多大?
(3)金属棒达到的稳定速度是多大?(4)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感强度逐渐减小,可使金属棒中不产生感应电流,则磁感强度B应怎样随时间t变化(写出B与t的关系式)?
随着越来越高的摩天大楼在各地的落成,至今普遍使用的钢索悬挂式电梯已经渐渐地不适用了.这是因为钢索的长度随着楼层的增高而相应增加,这样这些钢索会由于承受不了自身的重量,还没有挂电梯就会被扯断.为此,科学技术人员正在研究用磁动力来解决这个问题.如图所示就是一种磁动力电梯的模拟机,即在竖直平面上有两根很长的平行竖直轨道,轨道间有垂直轨道平面的匀强磁场B1和B2,且B1和B2的方向相反,大小相等,即B1= B2=1T,两磁场始终竖直向上作匀速运动.电梯桥厢固定在如图所示的一个用超导材料制成的金属框abcd内(电梯桥厢在图中未画出),并且与之绝缘.电梯载人时的总质量为5×103kg,所受阻力f=500N,金属框垂直轨道的边长Lcd=2m,两磁场的宽度均与金属框的边长Lac相同,金属框整个回路的电阻R=9.5×10-4Ω,假如设计要求电梯以v1=10m/s的速度向上匀速运动,那么,
(1)磁场向上运动速度v0应该为多大?
(2)在电梯向上作匀速运动时,为维持它的运动,外界必须提供能量,那么这些能量是由谁提供的?此时系统的效率为多少?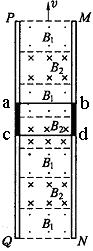
如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40Ω的电阻,质量为m=0.01kg、电阻为r=0.30Ω的金属棒ab紧贴在导轨上。现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,试求:
| 时间t(s) |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
| 下滑距离s(m) |
0 |
0.1 |
0.3 |
0.7 |
1.4 |
2.1 |
2.8 |
3.5 |
(1)当t=0.7s时,重力对金属棒ab做功的功率;
(2)金属棒ab在开始运动的0.7s内,电阻R上产生的热量;
(3)从开始运动到t=0.4s的时间内,通过金属棒ab的电量。
如图所示,空间存在垂直纸面向里的两个匀强磁场区域,磁感应强度大小均为B,磁场Ⅰ宽为L,两磁场间的无场区域为Ⅱ,宽也为L,磁场Ⅲ宽度足够大。区域中两条平行直光滑金属导轨间距为l,不计导轨电阻,两导体棒ab、cd的质量均为m,电阻均为r。ab棒静止在磁场Ⅰ中的左边界处,cd棒静止在磁场Ⅲ中的左边界处,对ab棒施加一个瞬时冲量,ab棒以速度v1开始向右运动。
(1)求ab棒开始运动时的加速度大小;
(2)ab棒在区域Ⅰ运动过程中,cd棒获得的最大速度为v2,求ab棒通过区域Ⅱ的时间;
(3)若ab棒在尚未离开区域Ⅱ之前,cd棒已停止运动,求:ab棒在区域Ⅱ运动过程中产生的焦耳热。
如图甲所示,匀强磁场方向垂直纸面向里,磁场宽度为 ,正方形金属框边长为
,正方形金属框边长为 ,每边电阻均为R/4,金属框以速度v的匀速直线穿过磁场区,其平面始终保持与磁感线方向垂直,当金属框cd边到达磁场左边缘时,匀强磁场磁感应强度大小按如图乙所示的规律变化.
,每边电阻均为R/4,金属框以速度v的匀速直线穿过磁场区,其平面始终保持与磁感线方向垂直,当金属框cd边到达磁场左边缘时,匀强磁场磁感应强度大小按如图乙所示的规律变化.
(1)求金属框进入磁场阶段,通过回路的电荷量;
(2)在图丙i-t坐标平面上画出金属框穿过磁场区的过程中,金属框内感应电流i随时间t的变化图线(取逆时针方向为电流正方向);
(3)求金属框穿过磁场区的过程中cd边克服安培力做的功W.
