满足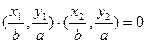 ,椭圆的离心率
,椭圆的离心率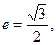 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.
(1)求椭圆的方程;
(2)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(3)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由
(本小题满分14分)下图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
,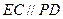 ,且
,且 ,
,
(1)求证:BE//平面PDA;
(2)若N为线段 的中点,求证:
的中点,求证: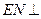 平面
平面 ;
;
(3)若 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.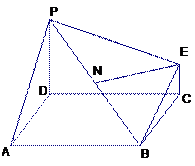
(本小题满分12分)已知下列两个命题: 函数
函数 在
在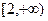 单调递增;
单调递增;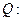 关于
关于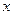 的不等式
的不等式
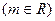 的解集为
的解集为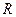 ;
;
若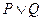 为真命题,
为真命题, 为假命题,求
为假命题,求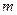 的取值范围.
的取值范围.
(本小题满分12分)若函数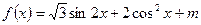 在区间
在区间 上的最大值为6,
上的最大值为6,
(1)求常数m的值及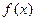 的对称中心;
的对称中心;
(2)作函数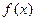 关于
关于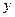 轴的对称图象得函数
轴的对称图象得函数 的图象,再把
的图象,再把 的图象向右平移
的图象向右平移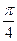 个单位得
个单位得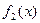 的图象,求函数
的图象,求函数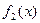 的单调递减区间.
的单调递减区间.
通过研究学生的学习行为,专家发现,学生的注意力随老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设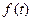 表示学生的注意力随时间
表示学生的注意力随时间 (分钟)的变化规律(注:
(分钟)的变化规律(注: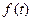 越大,表明学生的注意力越集中),经过实验分析得知:
越大,表明学生的注意力越集中),经过实验分析得知: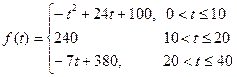 .
.
(1).讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2).讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3).一道数学难题需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
设函数y=f(x)是定义在R+上的减函数,并且满足f(xy)=f(x)+f(y), f(2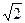 )=1,
)=1,
(1).求f(1)的值;
(2).求f(8)的值.
(3).如果f(4)+f(x-2)<2,求x的取值范围。