设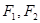 分别是椭圆:
分别是椭圆:  (
( )的左、右焦点,过
)的左、右焦点,过 斜率为1的直线
斜率为1的直线 与该椭圆相交于P,Q两点,且
与该椭圆相交于P,Q两点,且 ,
, ,
,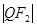 成等差数列.
成等差数列.
(Ⅰ)求该椭圆的离心率;
(Ⅱ)设点M(0,-1)满足|MP|=|MQ|,求该椭圆的方程.
已知抛物线C: 过点
过点 .
.
(Ⅰ)求抛物线C的方程,并求其准线方程;
(Ⅱ)是否存在平行于OM(O为坐标原点)的直线 ,使得直线
,使得直线 与抛物线C有公共点,且直线OM与
与抛物线C有公共点,且直线OM与 的距离等于
的距离等于 ?若存在,求直线
?若存在,求直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
设函数 在
在 及
及 时取得极值.
时取得极值.
(Ⅰ)求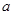 、
、 的值;
的值;
(Ⅱ)若对于任意的 ,都有
,都有 成立,求c的取值范围
成立,求c的取值范围
双曲线 的焦距为2c,直线
的焦距为2c,直线 过点(
过点( ,0)和(0,
,0)和(0, ),且点(1,0)到直线
),且点(1,0)到直线 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线 的距离之和
的距离之和 求双曲线的离心率e的取值范围.
求双曲线的离心率e的取值范围.
已知圆C: ,问是否存在斜率为1的直线
,问是否存在斜率为1的直线 ,使
,使 被圆C截得的弦为AB,以AB为直径的圆经过原点,若存在,写出直线
被圆C截得的弦为AB,以AB为直径的圆经过原点,若存在,写出直线 的方程;若不存在,说明理由
的方程;若不存在,说明理由