（本小题满分12分）点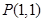
为椭圆
内的一定点，过P点引一直线，与椭圆相交于
两点，且P恰好为弦AB的中点，如图所示，求弦AB所在的直线方程及弦AB的长度。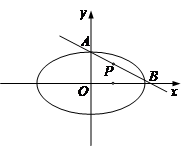
（本小题满分12分）已知双曲线的一条渐近线方程是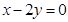
，若双曲线经过点
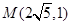，求此双曲线的标准方程。
（本小题两小题，每题6分，满分12分）
⑴对任意
，试比较
与
的大小；
⑵已知函数
的定义域为R，求实数k的取值范围。
（本小题满分10分）已知，三个数成等差数列，其和为6，若分别加上1，2，5之后成等比数列，求此三数。
已知,椭圆C以过点A(1,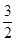
),两个焦点为(-1,0)(1,0)｡
(1)求椭圆C的方程;
(2)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值｡
，
（
）
时，函数
在其定义域是增函数，求b的取值范围。
，
，求函数
的最小值