(本小题满分12分)已知椭圆E的长轴的一个端点是抛物线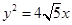 的焦点,离心率是
的焦点,离心率是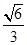
(1)求椭圆E的方程;
(2)过点C(—1,0),斜率为k的动直线与椭圆E相交于A、B两点,请问x轴上是否存在点M,使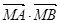 为常数?若存在,求出点M的坐标;若不存在,请说明理由.
为常数?若存在,求出点M的坐标;若不存在,请说明理由.
已知向量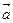 =(cos
=(cos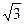 x,sin
x,sin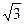 x),
x),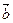 =(cos
=(cos ,sin
,sin )(0
)(0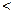

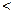
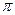 ).
).
设函数f(x)=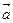 ·
·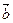 ,且f(x)+
,且f(x)+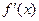 为偶函数.(1)求
为偶函数.(1)求 的值;
的值;
(2)求f(x)的单调增区间.
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos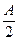 =
=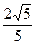 ,
,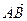 ·
·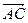 =3,若c=1,求a的值.
=3,若c=1,求a的值.
给出下列命题:
(1)存在实数 ,使sin
,使sin cos
cos =1;(2)存在实数
=1;(2)存在实数 ,使sin
,使sin +cos
+cos =
=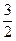 ; (3)y=sin(
; (3)y=sin(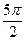 -2x)是偶函数;(4)x=
-2x)是偶函数;(4)x=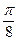 是函数y=
是函数y=  sin(2x+
sin(2x+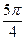 )的一条对称轴的方程;(5)若
)的一条对称轴的方程;(5)若 、
、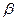 是第一象限角,且
是第一象限角,且
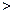
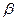 ,则sin
,则sin
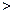 sin
sin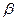 ;其中所有的正确命题的序号是 .
;其中所有的正确命题的序号是 .
如图,函数y=2sin( x+
x+ )(其中x
)(其中x R,0
R,0


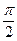 )
)
的图象与y轴交于点(0,1). (1)求 的值; (2)设P是图象
的值; (2)设P是图象
上的最高点,M、N是图象与x轴的交点,求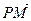 与
与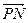 的夹角.
的夹角.
一根杆子长 ,任意地将其折成几段,如果折段点为(1)一个;(2)二个,而且杆子折段在任何位置是等可能的,试求每段杆子的长度均不少于10
,任意地将其折成几段,如果折段点为(1)一个;(2)二个,而且杆子折段在任何位置是等可能的,试求每段杆子的长度均不少于10 的概率。
的概率。