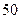
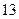
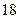

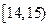
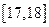
(Ⅰ)若成绩大于或等于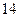 秒且小于
秒且小于 秒认为良好,求该班在这次百米测试中成绩良好的人数;
秒认为良好,求该班在这次百米测试中成绩良好的人数;
(Ⅱ)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于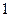 的概率。
的概率。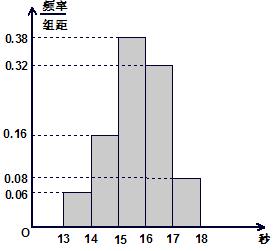
下面的茎叶图是某班在一次测验时的成绩,程序用同时统计女生、男生及全班成绩的平均分,试回答下列问题:
(1) 在程序中,“=0”的含义是什么?
横线①处应填什么?
(2) 执行程序,输出S,T,A的值分别是多少?
(3) 请分析该班男女生的习情况.
 已知数列
已知数列 中,
中, ,且
,且
 ,求这个数列的第m项
,求这个数列的第m项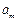 的值
的值 .现给出此算法流程图的一部分如图1,
.现给出此算法流程图的一部分如图1,
(1)请将空格部分(两个)填上适当的内容;
(2)用“For”循环语句写出对应的算法;
(3)若输出S=16,则输入的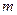 的值是多少?
的值是多少?
为了让生了解环保知识,增强环保意识,某中举行了一次“环保知识竞赛”,共有900名生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)若用系统抽样的方法抽取50个样本,现将所有生随机地编号为
000,001,002,…,899,试写出第二组第一位生的编号 ;
(2)填充频率分布表的空格(将答案直接填在表格内)和补全频率分布直方图
(3)所抽取的这些数据的中位数可能在直方图的哪一组?
(4)若成绩在75.5~85.5分的生为二等奖,估计获二等奖的生为多少人?
(本题12分)已知 .
.
(1)求函数 的定义域;
的定义域;
(2)判断函数 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)求使 的
的 的取值范围.
的取值范围.
(本题12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式.
(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能是企业获得最大利润,其最大利润约为多少万元(精确到1万元
