(1)从4名医生7名护士中选出2名医生4名护士分成两队,每队1名医生2名护士,到A、B两地巡回医疗,则不同的选取方法有多少种?
(2)一组同学共7人,从男生中选2人,女生中选2人,参加三种不同的活动,要求每人参加一种活动,且每种活动都有人参加,经计算,不同的选法共有648种,则该组中男、女生各有多少名?
设 ,函数
,函数 .
.
(Ⅰ)当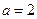 时,求函数
时,求函数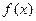 的单调增区间;
的单调增区间;
(Ⅱ)若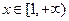 时,不等式
时,不等式 恒成立,实数
恒成立,实数 的取值范围
的取值范围
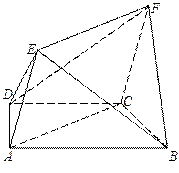
如图,多面体 中,
中, 是梯形,
是梯形, ,
,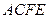 是矩形,面
是矩形,面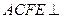 面
面 ,
, ,
,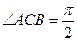 .
.
(1)若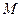 是棱
是棱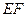 上一点,
上一点, 平面
平面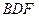 ,求
,求 ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
已知数列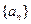 中,
中,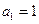 ,
,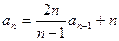
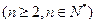 .且
.且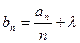 为等比数列。
为等比数列。
(1) 求实数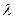 及数列
及数列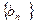 、
、 的通项公式;
的通项公式;
(2) 若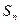 为
为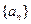 的前
的前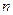 项和,求
项和,求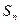 。
。
已知向量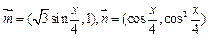 .
.
(1)若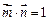 ,求
,求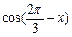 的值;
的值;
(2)记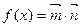 ,在△ABC
,在△ABC 中,角
中,角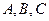 的对边分别是
的对边分别是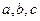 且满足
且满足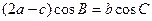 ,求函数f(A)的取值范围
,求函数f(A)的取值范围
已知曲线 上的动点
上的动点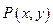 满足到点
满足到点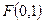 的距离比到直线
的距离比到直线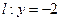 的距离小
的距离小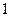 .
.
(1)求曲线 的方程;
的方程;
(2)动点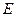 在直线
在直线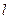 上,过点
上,过点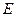 分别作曲线
分别作曲线 的切线
的切线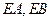 ,切点为
,切点为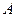 、
、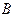 .
.
(ⅰ)求证:直线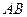 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线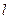 上是否存在一点
上是否存在一点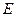 ,使得
,使得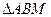 为等边三角形(
为等边三角形(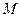 点也在直线
点也在直线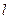 上)?若存在,求出点
上)?若存在,求出点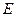 坐标,若不存在,请说明理由
坐标,若不存在,请说明理由