已知函数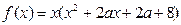 有三个零点
有三个零点 ,且
,且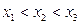 .
.
(1)求实数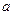 的取值范围;
的取值范围;
(2)记 ,求函数
,求函数 的值域.
的值域.
(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组
组成.
| 第一排 |
明文字符 |
A |
B |
C |
D |
| 密码字符 |
11 |
12 |
13 |
14 |
|
| 第二排 |
明文字符 |
E |
F |
G |
H |
| 密码字符 |
21 |
22 |
23 |
24 |
|
| 第三排 |
明文字符 |
M |
N |
P |
Q |
| 密码字符 |
1 |
2 |
3 |
4 |
设随机变量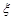 表示密码中所含不同数字的个数.
表示密码中所含不同数字的个数.
(Ⅰ)求 ;
;
(Ⅱ)求随机变量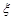 的分布列和它的数学期望.
的分布列和它的数学期望.
(本小题满分12分)已知△ABC的三内角A, B, C所对边的长依次为a,b,c,若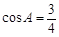 ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)若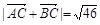 ,求△ABC的面积.
,求△ABC的面积.
(本小题12分)已知函数 .
.
(Ⅰ)若 在点(
在点( )处的切线方程为
)处的切线方程为 ,求实数
,求实数 的值;
的值;
(Ⅱ)当 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅲ)当 时,
时, 在区间
在区间 上恰有一个零点,求实数
上恰有一个零点,求实数 的取值范围.
的取值范围.
(本小题12分)已知椭圆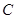 的中心在原点
的中心在原点 ,焦点在
,焦点在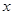 轴上,离心率为
轴上,离心率为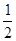 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为 .
.
(Ⅰ)求椭圆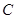 的标准方程;
的标准方程;
(Ⅱ)是否存在与椭圆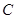 交于
交于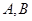 两点的直线
两点的直线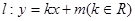 ,使得
,使得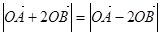 成立?若存在,求出实数
成立?若存在,求出实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
(本小题12分)如图,在棱长均为4的三棱柱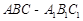 中,
中, 、
、 分别是
分别是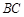 、
、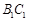 的中点
的中点
(1)求证: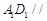 平面
平面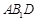 ;
;
(2)若平面ABC⊥平面BCC1B1,∠B1BC=60°,求三棱锥 的体积.
的体积.