数列 的前
的前 项和记作
项和记作 ,满足
,满足 ,
,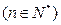 .
.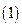 求出数列
求出数列 的通项公式.
的通项公式.
(2) ,且
,且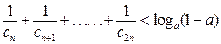 对正整数
对正整数 恒成立,求
恒成立,求 的范围;
的范围;
(3)(原创)若 中存在一些项成等差数列,则称
中存在一些项成等差数列,则称 有等差子数列,若
有等差子数列,若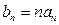 证明:
证明: 中不可能有等差子数列(已知
中不可能有等差子数列(已知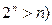 。
。
(满分12分)
设
(1)若 的取值范围;
的取值范围;
(2)若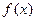 在区间[0,1]上的最小值为
在区间[0,1]上的最小值为 的值。
的值。
(满分12分)
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价P与上市时间t满足关系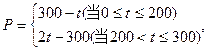 西红柿的种植成本Q与上市时间t满足关系
西红柿的种植成本Q与上市时间t满足关系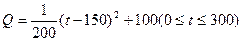 (市场售价与种植成本的单位是:元/100kg,时间单位是:天)。若认定市场售价减去种植成本为纯收益,问:何时上市的西红柿纯收益最大?
(市场售价与种植成本的单位是:元/100kg,时间单位是:天)。若认定市场售价减去种植成本为纯收益,问:何时上市的西红柿纯收益最大?
(满分12分)
设全集是实数集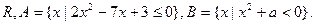
(1)当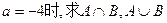 ;
;
(2)若 的取值范围。
的取值范围。
(满分12分)
已知关于x的不等式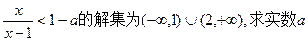 的值。
的值。
(本小题满分14分)
已知等差数列 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为 为等比数列,公比
为等比数列,公比 ;
;
(1)求 与
与 ;
;
(2)求数列 的前
的前 项和
项和 ;
;
(3)记 对任意正整数
对任意正整数 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。