判断其函数的奇偶性: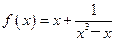
已知函数 在x=1处有极值10.
在x=1处有极值10.
(1)求a、b的值;
(2)求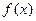 的单调区间;
的单调区间;
(3)求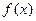 在[0,4]上的最大值与最小值。
在[0,4]上的最大值与最小值。
设方程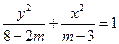 表示曲线C.
表示曲线C.
(1)m=5时,求曲线C的离心率和准线方程;
(2)若曲线C表示椭圆,求椭圆焦点在y轴上的概率。
双曲线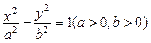 的左、右焦点分别为
的左、右焦点分别为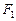 、
、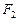 ,
, 为坐标原点,点
为坐标原点,点 在双曲线的右支上,点
在双曲线的右支上,点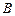 在双曲线左准线上,
在双曲线左准线上,
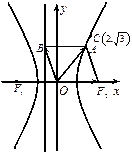
(Ⅰ)求双曲线的离心率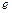 ;
;
(Ⅱ)若此双曲线过 ,求双曲线的方程;
,求双曲线的方程;
(Ⅲ)在(Ⅱ)的条件下, 、
、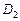 分别是双曲线的虚轴端点(
分别是双曲线的虚轴端点(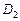 在
在 轴正半轴上),过
轴正半轴上),过 的直线
的直线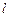 交双曲线
交双曲线 、
、 ,
,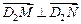 ,求直线
,求直线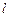 的方程
的方程
设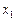 ,
, 是函数
是函数 的两个极值点,且
的两个极值点,且
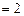 ..
..
(Ⅰ)用 表示
表示 ,并求
,并求 的最大值;
的最大值;
(Ⅱ)若函数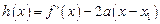 ,求证:当
,求证:当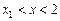 且
且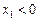 时,
时,
对于数列 ,定义
,定义 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 .
.
(Ⅰ)若数列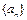 的通项公式
的通项公式 ,求
,求 的通项公式;
的通项公式;
(Ⅱ)若数列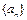 的首项是1,且
的首项是1,且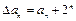 .
.
①设
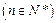 ,求数列
,求数列 的通项公式;
的通项公式;
②求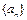 的前
的前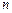 项和
项和 .
.