商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
如图,已知椭圆 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4( +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 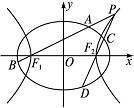
(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1·k2=1;
(3)是否存在常数λ,使得|AB|+|CD|=λ|AB|·|CD|恒成立?若存在,求λ的值;若不存在,请说明理由.
设函数 ,
, ,
, ,且以
,且以 为最小正周期.
为最小正周期.
(1)求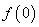 ;
;
(2)求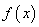 的解析式;
的解析式;
(3)已知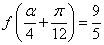 ,求
,求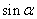 的值.
的值.
已知圆C与两坐标轴都相切,圆心C到直线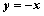 的距离等于
的距离等于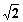 .
.
(1)求圆C的方程.
(2)若直线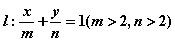 与圆C相切,求
与圆C相切,求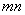 的最小值.
的最小值.
在锐角△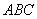 中,
中,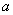 、
、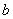 、
、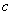 分别为角
分别为角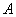 、
、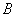 、
、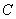 所对的边,且
所对的边,且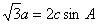
(1)确定角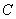 的大小;
的大小;
(2)若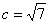 ,且△
,且△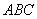 的面积为
的面积为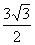 ,求
,求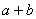 的值.
的值.
已知双曲线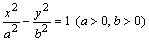 的右顶点为A,右焦点为F,右准线与
的右顶点为A,右焦点为F,右准线与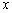 轴交于点B,且与一条渐近线交于点C,点O为坐标原点,
轴交于点B,且与一条渐近线交于点C,点O为坐标原点,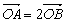 ,
, ,过点F的直线
,过点F的直线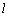 与双曲线右支交于点
与双曲线右支交于点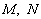 .
.
(Ⅰ)求此双曲线的方程;
(Ⅱ)求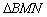 面积的最小值.
面积的最小值.