定义:若数列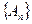 满足
满足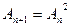 ,则称数列
,则称数列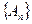 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列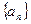 中,
中,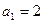 ,点
,点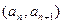 在函数
在函数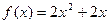 的图像上,其中
的图像上,其中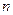 为正整数。
为正整数。
(1)证明:数列 是“平方递推数列”,且数列
是“平方递推数列”,且数列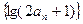 为等比数列。
为等比数列。
(2)设(1)中“平方递推数列”的前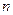 项之积为
项之积为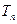 ,即
,即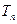
 ,求数列
,求数列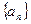 的通项及
的通项及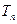 关于
关于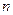 的表达式。
的表达式。
(3)记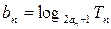 ,求数列
,求数列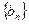 的前
的前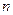 项之和
项之和 ,并求使
,并求使
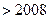 的
的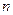 的最小值。
的最小值。
(本小题满分12分)
如图所示,某市准备在一个湖泊的一侧修建一条直路OC;另一侧修建一条观光大道,它的前一段OD是以O为顶点,x轴为对称轴,开口向右的抛物线的一部分,后一段DBC是函数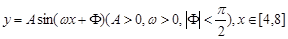 时的图象,图象的最高点为
时的图象,图象的最高点为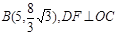 ,垂足为F。
,垂足为F。
(I)求函数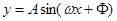 的解析式;
的解析式;
(II)若在湖泊内修建如图所示的矩形水上乐园PMFE,问点P落在曲 线OD上何处时,水上乐园的面积最大?
线OD上何处时,水上乐园的面积最大?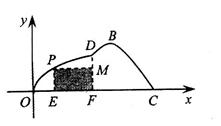
.(本小题满分12分)
将如图1的直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连结部分线段后围成一个空间几何体,如图2所示。
(I)证明:直线BE//平面ADF;
(II)求面FBE与面ABCD所成角的正切值。
(本小题满分12分)
在 ABC中,
ABC中,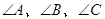 所对的边分别为a、b、c,且满足
所对的边分别为a、b、c,且满足
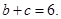
(I)求a的值;(II)求 的值。
的值。
(本小题满分12分)
已知数列 是等比数列,
是等比数列, 为其前n项和。
为其前n项和。
(I)设 ,求
,求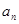 ;
;
(II)若 成等差数列,证明
成等差数列,证明 也成等差数列。
也成等差数列。
求与圆 外切且与直线
外切且与直线 相切于点
相切于点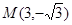 的圆的方程.
的圆的方程.