已知函数f(x)=alnx+bx2图象上点P(1,f(1))处的切线方程为2x-y-3=0.
(1)求函数y=f(x)的解析式;
(2)函数g(x)=f(x)+m-ln4,若方程g(x)=0在[ ,2]上恰有两解,求实数m的取值范围.
,2]上恰有两解,求实数m的取值范围.
水库的蓄水量随时间而变化,现用 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于 的近似函数关系式为
的近似函数关系式为
(1)该水库的蓄求量小于50的时期称为枯水期.以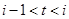 表示第1月份(
表示第1月份( ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?
(2)求一年内该水库的最大蓄水量(取 计算).
计算).
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
(1)证明:BD⊥AA1;
(2)求锐二面角D-A1A-C的平面角的余弦值;
(3)在直线CC1上是否存在点P,使BP∥平面DA1C1?若存在,求出点P的位置;若不存在,说明理由.
已知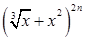 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x- )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以 ,
, 为边的平行四边形的面积;
为边的平行四边形的面积;
(2)若|a|= ,且a分别与
,且a分别与 ,
, 垂直,求向量a的坐标.
垂直,求向量a的坐标.