已知a，b，c为正实数，a+b+c=1. 求证:
(1)a2+b2+c2≥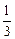
(2)
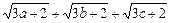≤6
在正三角形ABC的边AB、AC上分别取D、E两点，使沿线段DE折叠三角形时，顶点A正好落在边BC上，在这种情况下，若要使AD最小，求AD∶AB的值.
在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，且a、b、3c成等比数列，又∠A－∠C=
，试求∠A、∠B、∠C的值.
在△ABC中，a、b、c分别为角A、B、C的对边，
.
(1)求角A的度数；
(2)若a=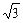
，b+c=3，求b和c的值.
如右图，在半径为R的圆桌的正中央上空挂一盏电灯，桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比，角和这一点到光源的距离r的平方成反比，即I=k·
，其中k是一个和灯光强度有关的常数，那么怎样选择电灯悬挂的高度h，才能使桌子边缘处最亮？
，使得
是以点E为直角顶点的等腰直角三角形。