将圆x2 + y2 + 2x – 2y = 0按向量a= (1，–1)平移得到圆O，直线l和圆O相交于A、B两点，若在圆O上存在点C，使
，且
=
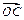a．
（1）求的值；（2）求弦AB的长；（3）求直线l的方程．
设
.
（1）当
时，
，求a的取值范围；
（2）若对任意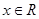
，
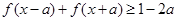恒成立，求实数a的最小值.
已知曲线C的极坐标方程为
，直线
的参数方程为
（t为参数，
）.
（1）把曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
（2）若直线经过点
，求直线被曲线C截得的线段AB的长.
如图，直线AB过圆心O，交
于F（不与B重合），直线
与相切于C，交AB于E，且与AF垂直，垂足为G，连结AC.
求证：（1）
；（2）
.
已知函数
.
（1）当
时，求
的极值；
（2）当
时，讨论的单调性；
（3）若对任意的
，
，恒有
成立，求实数
的取值范围.
已知圆
，直线
与圆
相切，且交椭圆
于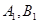
两点，c是椭圆的半焦距，
.
（1）求m的值；
（2）O为坐标原点，若
，求椭圆
的方程；
（3）在（2）的条件下，设椭圆的左右顶点分别为A，B，动点
，直线
与直线
分别交于M，N两点，求线段MN的长度的最小值.