已知定点A(a,O)( a >0),B为x轴负半轴上的动点.以AB为边作菱形ABCD,使其两对角线的交点恰好落在y轴上.
(I)求动点D的轨迹E的方程;
(Ⅱ)过点A作直线l与轨迹E交于P、Q两点,设点R (- a,0),问当l绕点A转动时,∠PRQ是否可以为钝角?请给出结论,并加以证明.
(本小题满分12分)
已知椭圆 的两个焦点分别为
的两个焦点分别为 、
、 ,短轴的两个端点分别为
,短轴的两个端点分别为 .
.
(Ⅰ)若 为等边三角形,求椭圆
为等边三角形,求椭圆 的方程;
的方程;
(Ⅱ)若椭圆 的短轴长为
的短轴长为 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,且
两点,且 ,
,
求直线 的方程.
的方程.
(本小题满分12分)
已知函数 .
.
(Ⅰ)当 时,求关于
时,求关于 的不等式
的不等式 解集;
解集;
(Ⅱ)当 时,若
时,若 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(本小题满分12分)
已知椭圆 :
: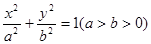 的离心率为
的离心率为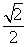 ,其中左焦点
,其中左焦点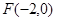 .
.
(Ⅰ)求椭圆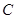 的方程;
的方程;
(Ⅱ)若直线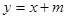 与椭圆
与椭圆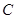 交于不同的
交于不同的 两点,且线段
两点,且线段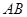 的中点
的中点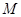 在圆
在圆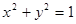 上,求
上,求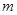 的值.
的值.
(本小题满分12分)
在等差数列 中,公差
中,公差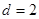 ,
,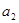 是
是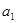 与
与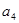 的等比中项.
的等比中项.
(Ⅰ)求数列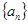 的通项公式;
的通项公式;
(Ⅱ)设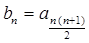 ,数列
,数列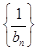 的前
的前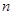 项和为
项和为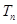 ,求
,求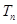 .
.
(本小题满分12分)
已知在等比数列 中,
中,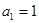 ,且
,且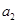 是
是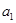 和
和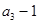 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列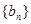 满足
满足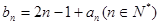 ,求
,求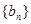 的前
的前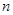 项和
项和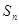 .
.