已知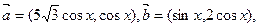 其中
其中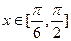 ,
,
设函数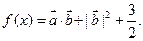
(Ⅰ)求函数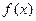 的的值域;
的的值域;
|
(Ⅱ)若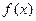 ="8," 求函数
="8," 求函数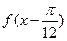 的值.
的值.
已知 ,
,
 求
求 及
及 .
.
将两副三角板放成如图所示的形状,使二面角D-AC-B成直二面角。
已知:BC=CD,∠ACD=∠ABC=900.求:二面角C-AB-D的大小。
在工厂生产中,若机器更新过早,则生产潜力未能充分发挥而造成浪费;若更新过迟,老机器生产效率低,维修与损耗费用大,也会造成浪费.因此,需要确定机器使用的最佳年限(即机器使用多少年平均费用最小)
某工厂用7万元购买了一台新机器,运输安装费2千元,每年投保、动力消耗固定的费用为2千元;每年的保养、维修、更换易损件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,……,即每年增加1千元,问这台机器的最佳使用年限是多少年?并求出年平均费用的最小值.
某企业在今年年初向银行贷款 万元,年利率为
万元,年利率为 ;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
;从今年年末开始,每年末向银行偿还一定的金额,预计五年内还清,问每年末平均偿还的金额应是多少?
进货原价为80元的商品400个,按90元一个售出时,可全部卖出。已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?