已知椭圆的中心在坐标原点,焦点在x轴上,它的一个焦点为F,M是椭圆上的任意点,|MF|的最大值和最小值的几何平均数为2,椭圆上存在着以y=x为轴的对称点M1和M2,且|M1M2|=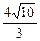 ,试求椭圆的方程
,试求椭圆的方程
在平面直角坐标系xOy中,直线l的参数方程为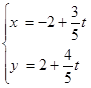
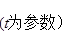 它与曲线C:
它与曲线C: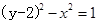 交于A、B两点。
交于A、B两点。
(1)求|AB|的长
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为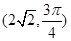 ,求点P到线段AB中点M的距离。
,求点P到线段AB中点M的距离。
已知 。
。
(1)若不等式 对任意实数
对任意实数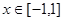 恒成立,求实数
恒成立,求实数 的取值范围;(2)若
的取值范围;(2)若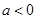 ,解不等式
,解不等式 。
。
某人上午7:00时,乘摩托车以匀速 千米/时
千米/时 从A地出发到相距50千米的
从A地出发到相距50千米的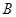 地去,然后乘汽车以匀速
地去,然后乘汽车以匀速 千米/时
千米/时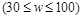 自
自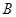 地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为
地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为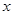 小时, 摩托车所需要的时间为
小时, 摩托车所需要的时间为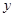 小时.
小时.
(1)写出满足上述要求的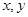 的约束条件;
的约束条件;
(2)如果途中所需的经费为 ,且
,且 (元),那么
(元),那么 ,
,  分别是多少时所要的经费最少?此时需花费多少元?
分别是多少时所要的经费最少?此时需花费多少元?
已知向量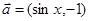
 ,函数
,函数
(1)求函数 的值域;
的值域;
(2)已知 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且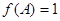 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组 ;第二组
;第二组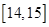 ……第五组
……第五组 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设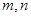 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知 求事件
求事件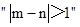 的概率.
的概率.