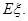已知函数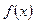 的定义域为R,且满足以下条件:1对任意的
的定义域为R,且满足以下条件:1对任意的 ,有
,有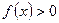 ;2对任意
;2对任意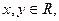 有
有 ;3
;3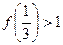
(Ⅰ)求 的值;
的值;
(Ⅱ)判断 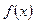 的单调性,并说明理由;
的单调性,并说明理由;
(Ⅲ)若 且a,b,c成等比数列,求证:
且a,b,c成等比数列,求证: .
.
设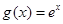 ,
, ,其中
,其中 是常数,且
是常数,且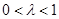 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数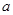 ,存在正数
,存在正数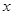 ,使不等式
,使不等式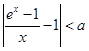 成立;
成立;
(3)设 ,且
,且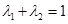 ,证明:对任意正数
,证明:对任意正数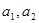 都有:
都有: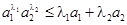 .
.
知数列 的首项
的首项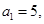 前
前 项和为
项和为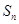 ,且
,且
(1)证明:数列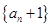 是等比数列;
是等比数列;
(2)令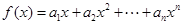 ,求函数
,求函数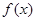 在点
在点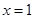 处的导数
处的导数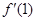 ,并比较
,并比较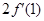 与
与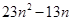 的大小.
的大小.
设椭圆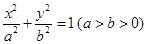 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率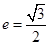 .过该椭圆上任一点
.过该椭圆上任一点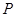 作
作 轴,垂足为
轴,垂足为 ,点
,点 在
在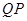 的延长线上,且
的延长线上,且 .
.
(1)求椭圆的方程;
(2)求动点 的轨迹
的轨迹 的方程;
的方程;
(3)设直线 (
( 点不同于
点不同于 )与直线
)与直线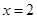 交于点
交于点 ,
,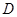 为线段
为线段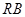 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
如图所示,已知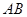 为圆
为圆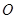 的直径,点
的直径,点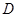 为线段
为线段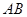 上一点,且
上一点,且 ,点
,点 为圆
为圆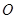 上一点,且
上一点,且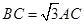 .点
.点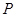 在圆
在圆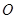 所在平面上的正投影为点
所在平面上的正投影为点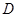 ,
, .
.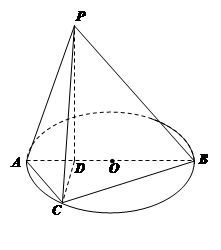
(1)求证: ;
;
(2)求二面角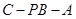 的余弦值.
的余弦值.
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7、8、9、10环,且每次射击成绩互不影响,射击环数的频率分布表如下: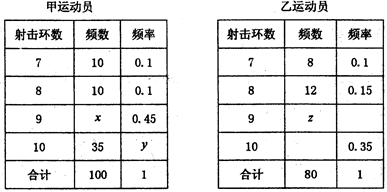
若将频率视为概率,回答下列问题:
(1)求表中x,y,z的值及甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次,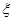 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求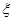 的分布列及
的分布列及